Sequential sampling and paradoxes of risky choice

Abstract

The common-ratio, common-consequence, reflection, and event-splitting effects are some of the best-known findings in decision-making research. They represent robust violations of expected utility theory, and together form a benchmark against which descriptive theories of risky choice are tested. These effects are not currently predicted by sequential sampling models of risky choice, such as decision field theory (Busemeyer & Townsend 1993). This paper, however, shows that a minor extension to decision field theory, which allows for stochastic error in event sampling, can provide a parsimonious, cognitively plausible explanation for these effects. Moreover, these effects are guaranteed to emerge for a large range of parameter values, including best-fit parameters obtained from preexisting choice data.

Introduction

Theories of sequential sampling and accumulation present one of the most successful approaches to studying decision-making. These theories predict behavior across a number of different psychological domains, using cognitive mechanisms that are biologically plausible and are also, in many cases, sophisticated enough to implement optimal speed-accuracy tradeoffs (see e.g. Bogacz, 2007; Gold & Shadlen 2007; Ratcliff & Smith 2004). Decision field theory (DFT) has applied the sequential sampling approach to modeling risky preferential choice(Busemeyer & Townsend 1993). In DFT, the available gambles are represented in terms of the rewards they provide to the decision-maker contingent on the occurrence of uncertain events. At each time step in the decision process, a feasible event is attended to probabilistically, with attention probability determined by the probability of the event. The outcomes of each of the available gambles, generated by the event, are subsequently evaluated, and accumulated into dynamic variables representing relative preferences. This process is repeated over time, until the relative preference for a gamble crosses a threshold value.

By using the sequential sampling approach to model risky decision-making, DFT is able to explain key findings involving decision times, time pressure and speed-accuracy tradeoffs, as well as violations of independence between alternatives and serial position effects on preference (Busemeyer & Townsend 1993; Busemeyer & -Diederich 2002; Dror, et al. 1999). Sequential sampling also allows DFT to capture violations of stochastic dominance with choices involving negatively correlated gambles, that is, gambles that offer divergent outcomes for the same event (Diederich & Busemeyer 1999; Busemeyer & Townsend 1993). Finally, extensions to DFT allow it to accommodate a number of behaviors pertaining to gamble pricing and related preference elicitation methods (Johnson & Busemeyer 2005).

These descriptive benefits are offset by DFT’s inability to account for well-known paradoxes of risky choice. These paradoxes, such as the common-ratio, common-consequence, reflection, and event-splitting effects, are some of the best-known and most studied findings on risky and uncertain decision-making. The common-consequence and common-ratio effects have, for example, been seen as providing strong evidence against expected utility theory since (Allais 1953). Both of these effects (as well as their reversal with the reflection effect) feature prominently in Kahneman and Tversky’s seminal prospect theory paper¹ Kahneman & Tversky (1979), as well as in more recent theory papers on risky choice (Brandstätter et al. 2006; Loomes 2010; Loomes & Sugden 1982; Machina 1987; Mukherjee 2010). Likewise event-splitting effects are now seen as providing strong evidence against prospect theory, and critics of prospect theory have used its inability to account for event-splitting effects to motivate newer descriptive theories of risky choice (see Birnbaum 2008) for a discussion).

DFT’s difficulty in explaining these paradoxes is due to the strong restrictions it imposes on the decision process. Unlike generalized utility models, which admit any unconstrained combination of non-linear probability weighting functions and non-linear utility functions, DFT assumes a fairly strict sequence of cognitive operations, with flexibility only in stochastic event attention, and the linear dynamics of preference accumulation. Common explanations for risky choice paradoxes, such as cumulative prospect theory’s (CPT) outcome-rank based probability weighting (Tversky & Kahneman 1992), are not easily accommodated within the sequential sampling and accumulation framework.

The goal of this paper is to explain these important risky paradoxes within the set of restrictions imposed by the sequential sampling and accumulation framework. Particularly, this paper presents a minor extension to decision field theory, which allows for stochastic errors in event attention. In the proposed model, attention probabilities are described by a mixture distribution. With some probability π, the decision-maker attends to events with probabilities equal to the events’ occurrence probabilities. However, with some probability 1 − π, the decision-maker gets distracted, and attends to events at random (that is, uniformly). For sufficiently high distraction probabilities, the proposed extension to decision field theory is able to generate the common-ratio effect, the common-consequence effect, the reflection effect, and event-splitting effects, thereby capturing four of the most important paradoxes of risky choice.

Explaining these paradoxes using DFT has a number of benefits. Firstly, it allows for some of the most studied findings in risky choice to be accommodated within the sequential sampling and accumulation framework, a framework that forms the basis of much theoretical inquiry on decision-making in psychology and neuroscience. Modifying DFT to explain these paradoxes can also be used to identify incorrect assumptions within DFT itself. Indeed this paper finds that allowing for the possibility of distraction not only explains highly specific paradoxes but also generates a significantly better quantitative fit to choice data over randomly generated gambles, compared to DFT without distraction. Finally, using DFT to explain risky paradoxes is useful for understanding the cognitive determinants of these behaviors. While alternate behavioral theories are equally powerful in describing choice, the mathematical manipulations stipulated by these theories are often too complex to be psychologically realistic. In contrast, the proposed model shows that probabilistic distraction, when added to a simple sequence of cognitive steps already known to be at play in decision-making, is sufficient to explain the many paradoxes of risky choice.

Model

Sequential sampling

The standard sequential sampling model presents decision-making as a dynamic, stochastic process, in which information regarding the responses in consideration is sampled probabilistically, and aggregated over time into one or more decision variables. These decision variables represent the relative support for the available responses, and decisions are made when one of these variables exceeds a threshold value. The dynamics of these variables can be formalized using random walks and diffusion processes, and sequential sampling models are able to make formal predictions regarding a number of different outcomes of the decision task, including choice probabilities, decision times, and post-choice confidence levels (Brown & Heathcote 2005; Busemeyer & Townsend 1993; Laming 1968; Pleskac & Busemeyer 2010; Ratcliff ; Ratcliff & Smith 2004; Usher & McClelland 2001; Wagenmakers, Van der Maas & Grasman 2007).

Accumulation processes involving one decision variable with two thresholds, or two perfectly and negatively correlated variables with one threshold each, are able to instantiate optimal speed–accuracy tradeoffs for a variety of sequential hypothesis tests (Bogacz, Brown, Moehlis, Holmes & Cohen 2006; Laming 1968). Sequential sampling models also provide a biologically inspired approach to studying decision-making: accumulation to threshold is a basic feature of individual neurons and neural networks, and computations corresponding to sequential information accumulation have been observed in human and animal brains (Gold & Shadlen 2007).

Due to these desirable mathematical, statistical, and biological properties, the sequential sampling and accumulation framework has been applied across a variety domains within psychology and neuroscience (Bogacz; Gold and Shadlen 2007). This framework has also been used to generate a number of unique insights with regards to preferential choice². When applied to this domain, sequential sampling models can explain behavioral findings as diverse as context dependence, reference dependence, response time effects, and speed–accuracy tradeoffs (Bhatia 2013; Busemeyer & Townsend 1993; Diederich 1997, Diederich 2003; Johnson & Busemeyer 2005; Krajbich, Armel & Rangel 2010; Roe, Busemeyer & Townsend 2001; Tsetsos, Chater & Usher; Usher & McClelland 2001).

Decision field theory

One of the earliest models of sequential sampling and accumulation in preferential choice is titled decision field theory (DFT). DFT is a theory of choice in risky and uncertain environments. Choice options, or gambles, within these environments are represented in terms of outcomes, contingent on probabilistic events, and decision-makers are required to select the gambles that they find most desirable. An example of a problem in this domain would involve the choice between a gamble in which the decision-maker wins $10 in the event that a coin flip lands heads and loses $10 in the event that a coin flip lands tails, and a gamble in which the decision-maker wins $5 in the event that a coin flip lands heads and loses $5 in the event that a coin flip lands tails. A more general setting would involve the choice between gambles x and y, yielding outcomes x ₁ and y ₁ in the event e ₁, outcomes x ₂ and y ₂ in the event e ₂, and so on. If there are N possible events, then we can write the probability of each event i as p _i > 0, with $\sum \nolimits _{i=1}^{N} p_{i} = 1$.

As in most other theoretical approaches to studying risky choice, the outcomes generated by a gamble are assumed to have a utility value. This is generally given by a function U(⋅), which maps a real-valued outcome (such as monetary payoff) onto a real-valued utility. We can write the vector of outcome utilities of x and y, generated by the N possible events, as U _x and U _y , respectively. With this notation, x has an expected utility of $\textbf {p} \cdot \textbf {U}_{x}^{T}$ and y has an expected utility of $\textbf {p} \cdot \textbf {U}_{y}^{T}$.

Axiomatic decision theory generally assumes that the preference for a gamble can be described by its expected utility (Savage 1954; Von Neumann & Morgenstern 1944). Common behavioral approaches to modeling risky choice, such as cumulative prospect theory, extend this approach by assuming that the weights on outcome utility are given by a nonlinear probability weighting function, which transforms probabilities based on their magnitudes and the relative ranks of the outcomes they are associated with (Tversky & Kahneman 1992). These approaches are both deterministic, as preference is described by a nonrandom variable, and static, as preference does not change across time. DFT in contrast is probabilistic and dynamic. It assumes that decision-makers attend to each event stochastically and sequentially, and accumulate utility differences between the outcomes of the available gambles for that event, into a relative preference variable. Relative preference changes stochastically over time, and choices are made when the relative preference variable crosses a threshold value.

More formally, DFT posits a stochastic weight vector w(t) = [w ₁(t), w ₂(t), ... , w _N (t)], which, for j ≠ i, is generally assumed to be described by the distribution:

$$ \text{Pr}[w_{i}(t) = 1 \text{ \& } w_{j}(t) = 0] = p_{i} $$

(1)

Note that w(t) is independent and identically distributed over time. We can thus write the expected weight vector at any time t as W = p.

At time t, the weight vector is multiplied by a vector of utility differences U = U _x − U _y , and added to the relative preference for x over y at t − 1, P(t − 1). This gives the relative preference for x over y at t, P(t), written as:

$$ P(t) = P(t-1) + \textbf{w}(t) \cdot \textbf{U}^{T} $$

(2)

The decision is generally assumed to begin with P(0) = 0, and terminate when P(t) crosses either an upper threshold θ > 0 or a lower threshold − θ < 0. If the upper threshold is crossed, then option x is selected, and if the lower threshold is crossed, then option y is selected. Additionally, the time to cross the threshold is equal to the decision time.

As an example of the decision process, consider a choice between a gamble x in which the decision-maker wins $10 in the event that a coin flip lands heads and loses $10 in the event that a coin flip lands tails, and a gamble y in which the decision-maker wins $5 in the event that a coin flip lands heads and loses $5 in the event that a coin flip lands tails. In deliberating between these gambles, the decision-maker would attend to the two possible events, the coin landing heads and the coin landing tails, sequentially. As these events are equally likely, each event would be sampled with the same probability. If heads is sampled, then the decision-maker’s relative preferences for x over y, P(t), would change by U(10) − U(5). If tails is sampled, then P(t) would change by U(−10) − U(−5). This would continue until either the upper threshold θ or the lower threshold − θ is crossed, that is until time t such that either P(t) > θ or P(t) < − θ.

Additional assumptions are also imposed on this framework (for psychological realism or mathematical tractability). For example, preferences are assumed to accumulate imperfectly, with decay, and a zero mean normally distributed noise term is assumed to add to the preference variable at each time period. The former assumption allows for a more flexible (but linear) time dependency in preference accumulation, whereas the latter assumption permits sources of noise other than probabilistic attention. When the above framework is combined with these assumptions, DFT is able to provide a comprehensive explanation for a range of behavioral findings not easily admissible by static, deterministic models of risky choice. These findings include violations of stochastic dominance caused by correlations between gamble outcomes, violations of independence caused by changes to gamble variance, serial position effects on preference, observed relationships between choice probability and decision time, and the observed effects of time pressure on decision accuracy (Busemeyer & Diederich 2002; Busemeyer & Townsend 1993; Diederich & Busemeyer 1999; Dror, et al. 1999).

Sampling with distraction

While decision field theory has a number of valuable descriptive and theoretical properties, it ultimately proposes that the rate of accumulation is equal to the expected difference in utility values of the two available options. Particularly, the expected change in preferences at each time period, E[P(t) − P(t − 1)] can simply be written as $\textbf {W} \cdot \textbf {U}^{T} = \textbf {p} \cdot \textbf {U}_{x}^{T} - \textbf {p} \cdot \textbf {U}_{y}^{T}$. This implies that preferences accumulate in favor of the gamble with the higher expected utility. When thresholds are not too small or certain simplifications regarding event sampling are made, this gamble is the one that is most likely to be chosen³. Subsequently, altering gambles x and y in such a way that the order of their expected utilities remains constant, does not change the modal choice predicted by DFT. DFT with additional assumptions, such as preference decay, generates a similar prediction. Particularly, the expected change in preference at time t, conditioned on P(t − 1), is an increasing linear function of the expected utility difference between the available options. Thus, as with the model presented here, DFT with preference decay predicts that the choice option with the higher expected utility will be more likely to be chosen.

Considerable behavioral evidence does however suggest that modal choices can change, even if the order of expected utility does not. Altering outcome probabilities, while keeping their relative ratios fixed, can affect choices despite the fact that this change does not alter the direction of the expected utility difference. A similar effect is observed when two identical, equally likely, outcomes of the two gambles are replaced with two other identical outcomes. Additionally, both these effects can be reversed for negative gamble outcomes. Finally, altering the presentation of the gambles by either joining or splitting their component outcomes (without affecting their expected utility) can affect modal choices. These findings, known as common-ratio, common-consequence, reflection, and event-splitting effects, provide strong evidence against theories that use expected utility to describe choice (Birnbaum 2008; Brandstätter et al. 2006; Kahneman & Tversky 1979; Loomes 2010; Loomes & Sugden 1982; Machina 1987; Mukherjee 2010; Starmer 2000). They also contradict the predictions of decision field theory, as it has been formalized and applied thus far (a more detailed discussion of these findings will be provided in subsequent sections)⁴.

We can avoid these problems by incorporating additional variability into event sampling. Variability in accumulation rates, starting points, and decision thresholds has been used by numerous sequential sampling models to explain response time and error/accuracy data in simple perceptual and lexical decisions (see e.g. Ratcliff & Smith 2004 for an overview). With regards to risky preferential choice, we can extend DFT by introducing variability, or stochastic error, in event attention. Particularly, even though attention probabilities should be equal to underlying event probabilities, we can assume that decision-makers occasionally get distracted, and attend to possible events at random (with a uniform probability). Attention can thus be described by a mixture distribution, in which attention sampling is driven by event probabilities, with some probability π, and determined by random, uniform sampling, with probability 1 − π. If we incorporate distraction into DFT, then for j ≠ i, we can modify Eq. 1 to write the probability distribution of the weight vector w(t) as:

$$ \text{Pr}[w_{i}(t) = 1 \text{ \& } w_{j}(t) = 0] = \pi \cdot p_{i} + (1 - \pi) \cdot d_{i} $$

(3)

with $d_{i}=\frac {1}{{n}}$

Here, i is some possible event, N is the total number of possible events, and d _i is the uniform probability of sampling event i if the decision-maker is distracted. The probability of attending to impossible events is assumed to be zero. Note again that w(t) is independent and identically distributed over time. The expected weight vector at any time t, is subsequently W = π ⋅ p+(1 − π)⋅d.

While we have assumed that d _i = 1/N—that is, distraction leads to uniform event sampling—this is by no means the only probabilistic specification of distraction that is compatible with our approach. Distraction could, for example, be driven by event salience or vividness, which in turn would depend on the contextual cues provided during the decision task (see e.g., Loewenstein, Weber, Hsee & Welch 2001), or event accessibility, which would depend on prior experiences with the available gambles (see e.g. Gonzalez, Lerch & Lebiere 2003). Decision-makers could also be distracted towards events with especially high or low outcomes, which would allow the model to approximate the transfer of attention exchange (TAX) model (e.g. Birnbaum 2008; Birnbaum and Chavez 1997). That said, uniform distraction seems to be a plausible and parsimonious first step to understanding the dynamics of event attention in DFT. Uniform distraction makes no assumptions about the decision environment or the decision-maker’s past experiences, but is fully compatible with alternative approaches designed to model the effect of these exogenous factors on risky behavior.

Overall distraction weakens the relatively strong assumption that event attention is determined entirely by event probability. If π = 1, then this assumption is satisfied and we obtain the standard DFT model. However, if π < 1 then event sampling is vulnerable to error. As π reduces, this error increases, and at π = 0 event attention is completely random, and every event is equally likely to be sampled. In this paper we will refer to the DFT model with π = 1 as standard DFT, and to the extended DFT model, which allows for π < 1 as distracted DFT.

Implications

Attention

Distraction can provide a simple explanation for the paradoxes that are a key feature of risky choice behavior. Although sampling errors are random in the sense that each event is equally likely to be sampled when the decision-maker is distracted, the effect of these errors is systematic. The rate of accumulation when π < 1 is not equal to the expected difference in utility values of the two available options. Altering the ratio of event probabilities, replacing identical outcomes, making outcomes negative, and splitting or combining events, can all affect the rate, and more importantly, the direction of accumulation, and subsequently reverse modal choice.

Distracted accumulation diverges from expected utility difference due to event attention. Distraction distorts an event’s attention probability away from its occurrence probability. As certain events are sampled more frequently under distraction, the accumulation of preferences is also changed. The specific effect of distraction on event attention, and subsequently on preference accumulation, depends on the events’ occurrence probabilities, p, and the total number of events in the task at hand, N. Recall that the expected attention weight vector at any time is given by W = π ⋅ p + (1 − π) ⋅ d. This implies that W _i is determined by the weighted combination of p _i and d _i = 1/N. If p _i < 1/N we get W _i > p _i for π < 1. In contrast, if p _i > 1/N we get W _i < p _i for π < 1.

We can draw out two implications from this. Firstly, unlikely events, with p _i < 1/N, will benefit from distraction, and the outcomes that these events generate will be of greater importance than would be justified by their occurrence probability. Intuitively, decision-makers are more likely to get distracted away from high probability events and attend to low probability events, than they are to do the opposite. Secondly, keeping p _i constant, increasing the total number of possible events will decrease the attention to event i. Intuitively, when decision-makers are distracted, they are less likely to attend to an event, if there are many other possible events to attend to.

The first of these implications can be interpreted as a form of probability weighting, one which resembles cumulative prospect theory’s overweighting of low probabilities and underweighting of high probabilities (Tversky & Kahneman 1992). That said, there are many crucial differences between the proposed distraction account of event attention and CPT’s probability weighting function. For example, CPT’s probability weighting function is insensitive to the number of events or outcomes that are possible for the available gambles. Allowing for additional outcomes in a gamble while keeping both the probability of an outcome j, and the cumulative probabilities of outcomes that are more desirable and less desirable than j constant, does not change the weight CPT places on j. In contrast, increasing the total number of possible events (and subsequently outcomes) necessarily reduces the attention probability of event i in the proposed distraction model. This plays an important role in allowing distracted decision field theory to account for violations of CPT’s predictions, such as event-splitting effects Birnbaum (2008). These violations will be discussed in subsequent sections.

A related difference pertains to the fact that CPT generally overweighs (underweighs) probabilities below (above) 0.33⁵

Another crucial difference pertains to the fact that decision field theory involves the sampling of events and not outcomes (see e.g. Busemeyer & Townsend 1993). It is the probabilities for these events that appear to be overweighted or underweighted by distraction. In contrast, CPT probability weighting affects only outcome probabilities. Subsequently, it its seldom the case that DFT and CPT distort the same probability values. This divergence allows DFT to capture a number of behaviors not possible with CPT, and additionally for these behaviors to be sensitive to distraction and its implied probability distortion.

There is one difference between the two theories that does not necessarily affect choice behavior. This pertains to psychological plausibility. The probability weighting function imposed by CPT assumes that decision-makers rank the outcomes of an available gamble, then, for an outcome j, take two sets of cumulative probabilities for outcomes that are superior to j and apply a sophisticated non-linear transformation to these cumulative probabilities, before subtracting one set of cumulative probabilities from the other, to determine the probability weight applied to outcome j. All outcomes across all available gambles are similarly weighted, before being aggregated into a utility measure, and the gamble with the highest weighted total outcome utility is selected (Tversky & Kahneman 1992). This is not the easiest way to weigh probabilities, and it is likely that decision-makers do not actually use this method while deliberating between gambles. Distracted DFT in contrast does not assume that decision-makers explicitly reweigh probabilities. Rather, it merely imposes non-systematic probabilistic error in event attention. This psychologically realistic assumption generates behavior corresponding to many of the best-known paradoxes in risky choice, behavior that can in some sense be understood in terms of biased probability weighting. Indeed, one interpretation of this is that distracted DFT provides a psychological justification for the probability weighting biases observed in decision-making research.

Note that the proposed account also resembles the transfer of attention exchange (TAX) model (Birnbaum 2008; Birnbaum & Chavez 1997). The TAX model assumes that attention is directed not only towards high-probability outcomes but also towards low-valued outcomes. This can generate risk-aversion, loss-aversion, as well as many other important phenomena in the domain of risky choice. While the predictions of distracted DFT and the TAX model converge in settings where low outcomes are generated with a low probability, there are many important differences between the two theories. Firstly, as with cumulative prospect theory, TAX assumes that gambles are evaluated in terms of their outcomes, and that the various paradoxes emerge from biased attention towards different types of outcomes rather than biased attention towards different events. DFT in contrast is an event based framework. Additionally, the TAX model assumes that attentional biases are systematic; that is, decision-makers explicitly direct their attention to some types of outcomes and not to others. In contrast, distraction in the proposed DFT model is not systematic. Every event is equally likely to be attended to when the decision-maker is distracted, and attentional biases and their associated paradoxes only emerge due to the complex interplay between non-systematic distraction and underlying event probabilities. Finally, the predictions of TAX and distracted DFT diverge strongly when low outcomes are not generated by low-probability events. In these settings, TAX and distracted DFT would predict different attention weights and subsequently different patterns of choice.

Behavior

What are the behavioral implications of distraction? In binary choice, increased attention towards low-probability events translates into an increased tendency to prefer the gamble that offers high outcomes for these events. This is often a risky gamble, and one effect of distraction is increased risk taking in such settings. If distraction is especially strong, then this can dominate the risk-aversion generated by concave utility, and generate risk-seeking behavior. Such behavior is often observed with lottery choices, where gambles that offer highly unlikely but highly desirable rewards are often chosen over certain payoffs with higher expected value. Note that these tendencies reverse when risky gambles offer highly negative (loss) outcomes for low-probability events. In these settings, the risk-seeking tendencies generated by concave utility in losses can be dominated by distraction, and decision-makers can instead display risk aversion.

Behaviorally, distraction can also generate changes in choice probabilities when gambles are altered in ways that do not affect their relative expected utility. The settings in which these changes are especially interesting involve the common-ratio, common-consequence, reflection, and event-splitting effects. In the remainder of this paper, we shall see how the behavioral implications of random distraction can provide a parsimonious, cognitively plausible explanation for these effects.

Testing fit: randomly generated gambles

Before we explore how probabilistic distraction explains highly specific paradoxes, let us first test whether it is a reasonable assumption in more general decision-making scenarios. Rieskamp (2008, study 2) presents a dataset of choices on randomly generated gambles. These gambles consist of 180 pairs of probabilistic outcomes involving both gains and losses (with values between -100 and 100 in experimental money units), and choices involving these gambles are elicited from 30 subjects. In this section, we fit both standard DFT and DFT with distraction to these choices, to examine whether distracted DFT provides a better fit to the data than standard DFT.

As in Rieskamp (2008), we use a simplification of decision field theory, which assumes that the change in preference is normally distributed (see also Busemeyer & Townsend 1993, pg 439-440). According to this simplification, the change in preference at time t is given by the following modified version of Eq. (2).

$$ P(t) = P(t-1) + \delta + \epsilon(t) $$

(4)

In Eq. (4), δ is equal to the expected sampling utility difference between x and y. More specifically, we have δ = W ⋅ U ^T, with W, the expected weight vector, derived from Eqs. 1 and 3. 𝜖 is a normally distributed error term with mean 0 and variance σ ². σ ², which is the variance of the sampling utility difference is specified as $\sigma ^{2} = {\sigma _{x}^{2}} + {\sigma _{y}^{2}} - 2 \cdot \sigma _{xy}$. Here, ${\sigma _{x}^{2}}$ is equal to the sampling variance of the utility of x, written as $\sum _{i=1}^{N} W_{i} \cdot [U(x_{i}) - \textbf {W} \cdot \textbf {U}_{x}^{T}]^{2}$. ${\sigma _{y}^{2}}$ is similarly defined, and σ _{x y} is equal to the sampling covariance between these two utilities, $\sum _{i=1}^{N} W_{i} \cdot [U(x_{i}) - \textbf {W} \cdot \textbf {U}_{x}^{T}] \cdot [U(y_{i}) - \textbf {W} \cdot \textbf {U}_{y}^{T}]$. Again, for ${\sigma _{x}^{2}}$, ${\sigma _{y}^{2}}$ and σ _{x y} , W, the expected weight vector, is derived from Eqs. 1 and 3. Preferences are assumed to accumulate to a threshold θ. This threshold, as in Rieskamp (2008), corresponds to θ ^∗/σ of the original model of Busemeyer & Townsend (1993), so that it is assumed that the decision-maker chooses a threshold θ ^∗ that is proportional to σ.

With this simplified form, we are able to analytically represent the choice probabilities for options x and y for any given threshold θ and any distraction probability 1 − π. This is given in Eq. 5 (which is taken from Eq. 3(c)in Busemeyer & Townsend 1993). Here, F is the logistic cumulative distribution function, given by F(z) = 1/[1 + e ^{− z}]. Note that this simplification retains the key features (such as the rate of preference accumulation) of the model outlined in the above section, while also permitting a closed form solution for choice probability and decision time. Such a derivation is very difficult without these simplifying assumptions (but see Busemeyer & Diederich 2002; Diederich 1997).

$$ \text{Pr}(x \text{ chosen}) = F\left[ \frac{2 \cdot \delta \cdot \theta}{\sigma} \right] $$

(5)

We assume that the utility function is non-linear and that it is described by a power function U(z) = z ^α for z ≥ 0 and U(z) = −( − z)^α for z < 0, with α constrained to the interval (0,1). This is a common assumption in decision modeling and has frequently been used when fitting risky choice data (e.g. Glockner & Pachur 2012; Nisson 2011; Stott 2006). For our purposes, allowing for non-linear utility does not alter the relative fits of standard DFT and distracted DFT to Rieskamp (2008) choice data. Additionally, non-linear utility cannot by itself provide an account for any of the risky paradoxes discussed in this paper. Non-linear utility does, however, allow us to use our fits to this data to make predictions regarding other choice sets, which present decision-makers with outcomes of much larger or much smaller magnitudes than the choices used in Rieskamp (2008).

With our assumption of non-linear utility, fitting standard DFT requires finding two parameters, θ and α, whereas fitting distracted DFT requires finding three parameters, θ, α, and π. Subsequently, standard DFT is nested in distracted DFT, and can be obtained by setting π = 1 in distracted DFT. We can thus determine whether distracted DFT provides a better fit than standard DFT by using the likelihood-ratio test, which tests whether allowing for π to vary leads to a significantly better likelihood value. The likelihood-ratio test statistic is written as D = − 2⋅[L _s − L _d ], where L _s and L _d are the log-likelihoods of standard DFT (π = 1) and distracted DFT (π flexible), respectively. D is distributed Chi-squared with one degree of freedom, corresponding to the one additional parameter in distracted DFT.

We can also compare the fits of the models using the Bayes information criterion (BIC). BIC asymptotically approximates a transformation of the Bayesian posterior probability of the candidate model, and in certain settings comparing two models using BIC is equivalent to model selection based on Bayes factor. The BIC for a model is formally defined as BIC = − 2∗ L + k⋅ln(n). Here, L is the best-fit log-likelihood of the candidate model, k is the number of free parameters in the model, and n is the number of observations the model is fit on. In model comparison, models with lower BIC are considered to have a better fit.

We fit standard DFT and distracted DFT to Rieskamp (2008) choice data using maximum likelihood estimation. Note that Rieskamp’s questions were represented in terms of outcome probabilities, and not in terms of the event probabilities underlying these outcome probabilities. DFT, as described by Busemeyer & Townsend (1993) and as outlined above, however, requires event probabilities. To fit Rieskamp’s data, we thus transformed the gambles in outcome space to equivalent gambles in event space, with the assumption that the outcomes of the two gambles were independent⁶. We fit both individual-level parameters and group-level parameters (in which observations across the 30 individuals were pooled together). In each fit we searched the parameter space to find the parameters that maximize the log-likelihood of the model on the data. This was done using a brute force search, with θ changing in increments of 0.05 in the interval [0,5], and α and π changing in increments of 0.01 in the interval [0,1]. The five best parameter values for each search were then used as starting points in an optimization routine using the simplex method. The parameter values yielding the highest log-likelihood out of these five simplex searches were considered the best-fit parameter values, and their corresponding log-likelihood was considered the best-fit log-likelihood value.

Our results indicate that distracted DFT does indeed provide a better fit to Rieskamp (2008) choice data than standard DFT. Particularly group-level estimations yield a best-fit log-likelihood value of -3,072.51 for distracted DFT compared to -3,200.56 for standard DFT⁷. This is a significant difference using the likelihood-ratio test (p < 0.01). Additionally, the BIC value for distracted DFT is 6,170.80, and the BIC value for standard DFT is 6,418.30, indicating a better fit for distracted DFT. The best-fit values of θ in standard DFT and distracted DFT are 0.89 and 1.45, respectively, the best-fit values of α in standard DFT and distracted DFT are 0.85 and 0.82, respectively, and the best-fit value of π in distracted DFT is 0.75. Note that we have a best-fit π < 1 indicating that decision-makers do, on average, get distracted during the decision process. Table 1 summarizes group-level fits for the two models.

Table 1 Summary of group-level model fits to Rieskamp (2008). L corresponds to the best-fit log-likelihood of the model and BIC is the Bayes information criterion value for this fit. Note that π = 1 is fixed (and not-estimated) for standard DFT

In fitting individual-level parameters to the choice data, we find that the choices of 19 out of the 30 subjects are better fit by distracted DFT than by standard DFT using the likelihood-ratio test. All these subjects have values of π that are significantly less than one (p < 0.05), and can be considered to be distracted while making their decisions. For the remaining 11 subjects, the fits of standard DFT and distracted DFT are similar, with the best-fit values of π not being significantly different to one (p > 0.05). The best-fit parameters of the subjects are displayed in Fig 1. Subjects who are better described by distracted DFT using the likelihood-ratio test are represented by black squares, and those that are not better described by distracted DFT are represented by white circles.

Fig. 1

Best-fit parameters for subjects in Rieskamp (2008). Black squares represent subjects for which distracted DFT offers a significantly better fit (p < 0.05), and white circles represent subjects for which distracted DFT does not offer a significantly better fit (p > 0.05), using the likelihood-ratio test

Note that three of the 11 subjects that are not better fit by distracted DFT have best-fit values of θ very close to zero. These subjects seem to be choosing randomly, and thus their fit to distracted DFT is not much better than their fit to standard DFT (indeed their fit to both these DFT models is quite weak). Out of the remaining eight subjects, half have a better (but statistically insignificant) fit with distracted DFT compared to standard DFT, with relatively large values of D, and a significance level of p < 0.15, whereas the other half are equally fit by standard and distracted DFT, and have negligible values of D, accompanied by p > 0.5.

When using the Bayes information criterion we find that 15 of the 30 subjects are better fit with distracted DFT compared to standard DFT. Overall, the median and average BIC values across subjects for standard DFT are 211.94 and 206.30, whereas the median and average BIC values for distracted DFT are 193.71 and 197.71, indicating once again that distracted DFT provides a better fit on the individual level (as well as on the group level).

Explaining risky paradoxes

The above section shows that permitting distraction within DFT, according to which decision-makers occasionally attend to events at random (that is, uniformly), allows for a better fit to choice data relative to DFT without distraction. Beyond this, allowing for distraction weakens the fairly strong assumption that event sampling probabilities are equal to their actual occurrence probabilities, and that the direction of accumulation, and subsequently the modal choice, is determined entirely by the relative expected utilities of the available options.

This can allow DFT to explain a number of risky choice paradoxes, such as the common-consequence effect, the common-ratio effect, the reflection effect, and event-splitting effects. Scholars of risky and uncertain decision-making have been studying these paradoxes for many decades (Birnbaum 2008; Brandstätter et al 2006; Kahneman and Tversky 1979; Loomes 2010; Loomes & Sugden 1982; Machina 1987; Mukherjee 2010; 2000). They provide important insights regarding deviations from the main assumptions of decision theory (Savage 1954; Von Neumann & Morgenstern 1944), and have been used extensively to compare the descriptive validity of different behavioral models of risky choice. In the simplification to standard DFT, introduced in Section 3, the option most likely to be chosen in the absence of distraction is the one with the highest expected utility. This is also the case for the more complex model, introduced in Section 2, as long as thresholds are not very small. This means that altering a choice problem while keeping the order of expected utilities of the two gambles constant does not alter standard DFT’s predicted modal choice. Risky paradoxes violate this property, and are thus not admissible within standard DFT. DFT with distraction, however, allows this property to be occasionally violated, thereby permitting these paradoxes. The remainder of this paper will discuss the precise mechanisms underlying these violations, and will show that these risky paradoxes are generated by distracted DFT for a very large range of parameters (including the best-fit parameters from the model fit in Section 3).

Expected utility theory

The risky choice paradoxes studied in this section are considered paradoxes because they violate the predictions of expected utility theory (EUT). EUT, initially proposed by Von Neumann & Morgenstern (1944), is one of the most elegant models of preferential choice. It assumes⁸ that gambles are evaluated entirely in terms of their expected utility, and that the gamble with the highest expected utility out of the set of available gambles is the one that is selected. The expected utility of a gamble x offering outcomes (x ₁, x ₂, ... x _M ) with outcome probabilities (q ₁, q ₂, ... q _M ) is written as $U(x) = \sum \limits _{j=1}^{M} q_{j} \cdot U(x_{j})$.

More general approaches, such as Savage’s (1954) subjective expected utility framework, present the available gambles in terms of events instead of outcomes. Particularly, a gamble (such as x) is described in terms of outcomes (x ₁, x ₂, ... x _N ) contingent on events (e ₁, e ₂, ... e _N ), with (potentially subjective) event probabilities given by (p ₁, p ₂, ... p _N ). As with EUT, these approaches also assume that gambles are evaluated entirely in terms of their expected utility, and that the gamble with the highest expected utility out of the set of available gambles is the one that is selected. The expected utility of a gamble, x, can be written as $U(x) = \sum \limits _{i=1}^{N} p_{i} \cdot U(x_{i})$. If the outcomes generated by the available gambles, as described in the EUT framework, are independent, then the expected utility in the outcome-based EUT framework and the more general event-based framework are identical, with one framework translating easily into the other. For example, two independent gambles, x and y, offering outcomes (x ₁, x ₂) with outcome probabilities (q ₁, q ₂) and outcomes (y ₁, y ₂) with outcome probabilities (r ₁, r ₂), can be equivalently be seen as offering outcomes (x ₁, x ₂, x ₁, x ₂) and (y ₁, y ₁, y ₂, y ₂) with event probabilities (q ₁ ⋅ r ₁, q ₂ ⋅ r ₁, q ₁ ⋅ r ₂, q ₂ ⋅ r ₂). Note that DFT is an event-based framework, but many of the paradoxes discussed in this paper (which have been formulated in response to EUT) present the available gambles in terms of independent outcomes. We will thus be transforming across the two gamble representations quite frequently for the remainder of the paper.

EUT and related expected utility-based frameworks are mathematically very tractable, and are thus the most commonly used risky decision models in economics and related social sciences (see Mas Colell, Whinston & Green (1995) for an overview of applications). These frameworks are also derived from very reasonable axioms about individual choice, and are thus considered to be models of rational decision-making. Individual behavior does, however, violate many of the predictions of expected utility maximization. Studying these violations yields a number of insights regarding the psychological processes underlying decision-making, and accounting for these violations is an important challenge for any cognitive model of risky choice.

Common-ratio effect

According to EUT, the utilities of the available outcomes are weighted by the probabilities of these outcomes, and added into an expected utility measure which determines choice. Subsequently, changing outcome probabilities while preserving their relative ratios should not alter the relative expected utility of the available gambles, and thus should not affect choice. This property also holds for other models, such as standard DFT, for which modal choice is often predicted by expected utility. According to standard DFT, altering outcome probabilities while maintaining their relative ratios would not affect the direction of accumulation, and modal choices will be the same for all gamble sets with the same outcome probability ratios.

As an example of this property, consider the decision between a gamble x that offers a gain of $3,000 with certainty, and a gamble y that offers a gain of $4,000 with probability 0.8, and a gain of $0 otherwise. If x is chosen over y, then EUT and standard DFT predict that the gamble x′ that offers a gain of $3,000 with probability 0.25 and a gain of $0 otherwise, should be chosen over the gamble y′ that offers a gain of $4,000 with probability 0.2 and a gain of $0 otherwise. This is because x′ and y′ have identical outcomes to x and y, and also have probabilities with a common-ratio to x and y (as 1/0.8 = 0.25/0.2). The opposite of this prediction is, however, observed empirically. Using the above gamble pairs, Kahneman and Tversky (1979) found that 80 % of respondents chose x over y, but only 35 % of respondents chose x′ over y′.

Distracted DFT can explain this choice pattern. Because of distraction, altering outcome probabilities while maintaining their relative ratios can affect the direction of accumulation and subsequently reverse modal choice. Decision-makers, according to DFT, would represent the choice between x and y in terms of two possible events⁹: gamble x giving $3,000 and gamble y giving $4,000, with event probability 0.8, and gamble x giving $3,000 and gamble y giving $0, with event probability 0.2 (an event involving gamble x giving $0 would not be considered, as this event is impossible). The decision-maker would focus mostly on the first event, as it has a higher probability. However due to distraction, the second event would be sampled more than 20 % of the time. Overall if distraction is strong enough, the high outcome difference caused by the second event would be sufficient to generate a higher choice probability for x.

This would not necessarily be the case for the choice between x′ and y′. This choice would be represented in terms of four events: gamble x′ giving $3,000 and gamble y′ giving $4,000, with event probability 0.05, gamble x′ giving $3,000 and gamble y′ giving $0, with event probability 0.2, gamble x′ giving $0 and gamble y′ giving $4,000, with event probability 0.15, and gamble x′ giving $0 and gamble y′ giving $0, with event probability 0.6. Now distraction ensures that the fourth event is sampled less frequently than its occurrence probability, and that the three remaining events are sampled more frequently than their occurrence probability. Out of these three events, two (i.e., event one and event three) yield higher outcomes for gamble y′ compared to gamble x′. If distraction is strong enough, then the outcome differences caused by these events would be sufficient to generate a higher choice probability for y′.

Indeed we can show that for the gamble pairs presented here, group-level distracted DFT parameters estimated on Rieskamp (2008) data would generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. This would not be the case were we to constrain π = 1, as with standard DFT. We obtain similar results with individual-level fits on Rieskamp’s data. Particularly, we can show that 19 of the 30 individuals from Rieskamp’s experiment, fit using distracted DFT, generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. None of the these individuals can generate this pattern of choice when fit using standard DFT.

Common-consequence effect

Another violation of expected utility theory is known as the common-consequence effect. EUT assumes that choice options with the highest expected utility are selected. As expected utility is calculated by weighing and adding outcome magnitudes, common outcomes, which occur with the same probability across all gambles, should be ignored. Changing these outcomes does not change the expected utility differences between gambles, and thus can not affect choice. This property also holds for other models, such as standard DFT, for which choice is often predicted by expected utility. According to standard DFT, altering common outcomes would not affect the direction of accumulation, or subsequently modal choice.

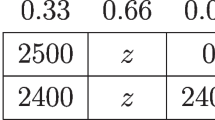
As an example of this property, consider the decision between a gamble x that offers a gain of $2,400 with certainty, and a gamble y that offers a gain of $2,500 with probability 0.33, a gain of $2,400 with probability 0.66, and a gain of $0 otherwise. Note that x can be seen as offering $2,400 with probability 0.34 and also offering $2,400 with probability 0.66. Hence getting $2,400 with probability 0.66 is a common consequence of the two gambles. EUT and standard DFT predict that this consequence should not affect modal choice. Replacing $2,400 with another outcome, such as $0, so as to generate a different common consequence should not change the decision-maker’s preferences. Hence if x is chosen over y in the above example, it should also be the case that the gamble x′ offering a gain of $2,400 with probability 0.34 and a gain of $0 otherwise, should be chosen over the gamble y′ offering a gain of $2,500 with probability 0.33 and a gain of $0 otherwise. This however is not what is observed. Using the above gamble pairs, Kahneman & Tversky (1979) found that 82 % of respondents chose x over y, but only 17 % of respondents chose x′ over y′.

Can distracted DFT explain this? Yes it can. Because of event based distraction, altering common outcomes can affect the direction of accumulation and subsequently reverse modal choice. Decision-makers, according to DFT, would represent the choice between x and y in terms of three possible events: gamble x giving $2,400 and gamble y giving $2,500, with event probability 0.33, gamble x giving $2,400 and gamble y giving $2,400, with event probability 0.66, and gamble x giving $2,400 and gamble y giving $0, with event probability 0.01 (an event involving gamble x giving $0 would not be considered as this event is impossible). The decision-maker would focus mostly on the second event, as it has a higher probability. However due to distraction, the third event would be sampled more than 1 % of the time (distraction will not affect attention to the first event for which p _i = 1/N = 1/3). Overall, if distraction is strong enough, the high outcome difference caused by the third event would be sufficient to generate a higher choice probability for x.

This would not necessarily be the case for the choice between x′ and y′. This choice would be represented in terms of four events: gamble x′ giving $2,400 and gamble y′ giving $2,500, with event probability 0.11, gamble x′ giving $2,400 and gamble y′ giving $0, with event probability 0.23, gamble x′ giving $0 and gamble y′ giving $2,500, with event probability 0.22, and gamble x′ giving $0 and gamble y′ giving $0, with event probability 0.44. Now distraction ensures that the fourth event is sampled less frequently than its occurrence probability, and that the three remaining events are sampled more frequently than their occurrence probability. Out of these three events, two (i.e., event one and event three) yield higher outcomes for gamble y′ compared to gamble x′. If distraction is strong enough then the outcome differences caused by these events would be sufficient to generate a higher choice probability for y′.

Indeed we can show that for the gamble pairs presented here, group-level distracted DFT parameters estimated on Rieskamp’s (2008) data would generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. This would not be the case were we to constrain π = 1, as with standard DFT. We obtain similar results with individual-level fits on Rieskamp’s data. Particularly, we can show that 22 of the 30 individuals from Rieskamp’s experiment, fit using distracted DFT, generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. None of the these individuals can generate this pattern of choice when fit using standard DFT.

Reflection effect

The common-ratio and common-consequence effects are the best known violations of expected utility theory’s predictions, and have been studied in numerous experimental settings. Although these effects are extremely robust for gambles consisting of positive outcomes, or gains, they have been shown to reverse with gambles consisting of negative outcomes, or losses.

Consider, for example, the decision between a gamble x that offers a loss of $3,000 with certainty, and a gamble y that offers a loss of $4,000 with probability 0.8, and a loss of $0 otherwise, and the parallel decision between a gamble x′ that offers a loss of $3,000 with probability 0.25 and a loss of $0 otherwise, and a gamble y′ that offers a loss of $4,000 with probability 0.2 and a loss of $0 otherwise. Kahneman and Tversky (1979) find that 92 % of respondents chose y over x, but only 42 % of respondents chose y over x′, indicating a violation of both expected utility theory and standard DFT. Note that these gambles are mirror images of the common-ratio gambles described above, for which Kahneman and Tversky (1979) have found the opposite modal choice pattern.

Although not studied in Kahneman and Tversky (1979), similar results also hold for the common-consequence effect. Using a different set of gambles Weber (2007) has shown that the common-consequence effect reverses when the gambles are reflected around the origin. Thus, with the gamble sets described above, these results suggest that a gamble y that offers a loss of $2,500 with probability 0.33, a loss of $2,400 with probability 0.66, and a loss of $0 otherwise would be, on average, selected over a gamble, x that offers a loss of $2,400 with certainty, but that a gamble x′ offering a loss of $2,400 with probability 0.34 and a loss of $0 otherwise, should be chosen over the gamble y′ offering a loss of $2,500 with probability 0.33 and a loss of $0 otherwise.

Both these sets of results are generated by distracted DFT. According to distracted DFT, the common-ratio and common-consequence effects are caused by distraction, which affects the sampling of the events involved in the available gambles. Reversing the sign of the outcomes generated by these events does not affect these attentional biases; it merely reverses the direction that the accumulating preference moves when these events are sampled. Thus a preference for a gamble x over a gamble y, when the outcomes are positive, can be reversed by making the outcomes of these gambles negative.

Indeed we can show that for both the common-ratio and the common-consequence reflection effects, group-level distracted DFT parameters estimated on Rieskamp’s (2008) data would generate a modal choice for y from the gamble pair consisting of x and y, and a modal choice of x′ from the gamble pair consisting of x′ and y′. This would not be the case were we to constrain π = 1, as with standard DFT. We obtain similar results with individual-level fits on Rieskamp’s data. For these individual-level fits, the same subjects that generated the standard common-ratio and common-consequence effects, would also generate their reversals with the reflection effect.

Event-splitting effect

A final paradox discussed in this paper is known as the event-splitting effect. As with the common-ratio and common-consequence effects, this effect demonstrates violations of the additive probability weighting assumption, which is the defining characteristic of expected utility theory. According to EUT, altering the presentation of a gamble so that the probability of a single outcome is split, and that outcome is represented as two equal outcomes (with the cumulative probability equal to that of the outcome in the initial presentation) should not affect the decision-maker’s expected utility for the gamble, or, subsequently, the choice between that gamble and other gambles. This property also holds for other models, such as standard DFT, for which modal choice is often predicted by expected utility. According to standard DFT, splitting an outcome would not affect the direction of accumulation, or subsequently modal choice. Cumulative prospect theory (although it does not assume expected utility) also predicts that event-splitting should not have an effect on choice (Birnbaum 2008).

Consider for example, the choice between a gamble x that offers a gain of $100 with probability 0.85 and a gain of $50 with probability 0.15, and a gamble y that offers a gain of $100 with probability 0.95, and a gain of $7 with probability 0.05. If choice is determined only by expected utility, then splitting the $50 outcome in x to generate a new gamble x′ that offers a gain of $100 with probability 0.85 and a gain of $50 with probability 0.10, and another gain of $50 with probability 0.05 should not affect the decision-maker’s preferences. Likewise splitting the $100 outcome in y to generate a new gamble y′ that offers a gain of $100 with probability 0.85, another gain of $100 with probability 0.10, and a gain of $7 with probability 0.05, should not affect final choice. Birnbaum (2004) however found that 74 % of decision-makers chose x over y, but only 38% of decision-makers chose x′ over y′. In general, splitting a high valued outcome, such as $100 in y, increases the relative preference for the gamble, but splitting a low valued outcome, such as $50 in x, decreases the relative preference for the gamble.

As with the common-ratio, common-consequence, and reflection effects, distracted DFT is able to explain event-splitting effects. Particularly, splitting an outcome into two or more component outcomes increases the number of events involving that outcome, subsequently increasing the likelihood that the decision-maker would get distracted and attend to an event generating the outcome. This increases the outcome’s weight in the gamble. If the outcome has a high value, then the gamble appears more desirable to the decision-maker. In contrast, if the outcome has a low value, then the gamble appears less desirable to the decision-maker.

More specifically, decision-makers, according to DFT, would represent the choice between x and y in terms of four possible events: gamble x giving $100 and gamble y giving $100, with event probability 0.81, gamble x giving $100 and gamble y giving $7, with event probability 0.04, gamble x giving $50 and gamble y giving $100, with event probability 0.14, and gamble x giving $50 and gamble y giving $7, with event probability 0.01. Here the first event would be sampled the most frequently, but, due to distraction, would be sampled less frequently than its actual occurrence probability. Out of the remaining three events, two (i.e., event two and event four) yield higher outcomes for gamble x compared to gambles y. If distraction is strong enough then the outcome differences caused by these events would be sufficient to generate a higher choice probability for x.

This would not necessarily hold for choices between x′ and y′. This choice would be represented in terms of nine events, out of which eight events would be oversampled relative to their occurrence probability. Out of these eight events four generate a higher outcome for y′, three generate a higher outcome for x′, and one generates the same outcomes for x′ and y′. Thus if distraction is strong enough then the outcome differences caused by the four events supporting y′ would be sufficient to generate a higher choice probability for y′.

Indeed we can show that for the gamble pairs presented here, group-level distracted DFT parameters estimated on Rieskamp’s (2008) data would generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. This would not be the case were we to constrain π = 1, as with standard DFT. We obtain similar results with individual-level fits on Rieskamp’s data. Particularly, we can show that 22 of the 30 individuals from Rieskamp’s experiment, fit using distracted DFT, generate a modal choice for x from the gamble pair consisting of x and y, and a modal choice of y′ from the gamble pair consisting of x′ and y′. None of the these individuals can generate this pattern of choice when fit using standard DFT.

Note that distracted DFT predicts that these event-splitting effects should also reverse when they contain negative outcomes, that is, that the reflection effect should extend to gambles generated to test event-splitting. This happens for the same reason that the common-ratio and common-consequence effects reverse for negative outcomes. Particularly, changing the sign of the outcomes generated by various gambles does not affect the attentional biases responsible for event-splitting effect, rather it reverses the direction that the accumulating preferences move when these events are sampled. Thus the preference for gamble x over y and the preference for gamble y′ over x′ when the outcomes are positive, can be reversed by making the outcomes negative. To our knowledge, this has not been tested thus far.

Testing fit: paradox gambles

Section 4 has shown that distracted DFT is able to generate many of the best known paradoxes in risky choices. These effects include standard violations of expected utility, as well as additional findings such as the event-splitting effect, not easily accommodated by cumulative prospect theory and related approaches. The discussion of these effects in Sec 4, is, however, qualitative (involving modal choices instead of actual choice probabilities). It is unclear how much better distracted DFT is compared to standard DFT in accounting for these findings, and additionally whether distracted DFT is even able to provide a comprehensive explanation for these effects for a plausible range of parameter values. The model fits to Rieskamp’s (2008) data are useful for demonstrating the superiority of distracted DFT in general settings, but do not provide a strong enough test of the theory for the specific types of anomalies explored in this paper.

In order to address these issues we must fit distracted DFT to a gamble set formulated specifically to test risky paradoxes. One candidate for this is Kahneman and Tverksy’s (1979) influential prospect theory dataset. This dataset consists of 1064 responses for a total of 14 single-stage monetary gamble pairs¹⁰. Some of the gamble pairs described in the above sections are obtained from this dataset. In this section we will use all of the gamble pairs in this dataset to compare standard and distracted DFT. As above we will fit the two models described in Section 3 using maximum likelihood estimation, and compare these models using their relative log-likelihood values, as well as the likelihood-ratio test and the Bayes information criterion.

We can first check how well our existing distracted DFT parameters (estimated on Rieskamp’s (2008) data) predict responses in this dataset. We find that standard DFT has a log-likelihood value of -722.80, and that distracted DFT has a log-likelihood value of -649.63, when fit using the parameters estimated in Section 3 and presented in Table 1. Additionally, for these parameters, standard DFT can predict the modal choice in only seven out of the 14 gambles, whereas distracted DFT can predict the modal choice in 12 out of the 14 gambles.

It is possible to improve this fit. Fig. 2 displays the values of the π and α parameters that are able to predict the modal choice in all of 14 gambles in Kahneman and Tversky’s dataset. Note that parameter combinations with π = 1 are unable to predict all modal choices, though high values of π can do this given suitable values of α. Also note that these results are independent of the threshold parameter θ as this parameter does not affect modal choice probabilities.

Fig. 2

Values of π and α that can predict the modal choice in all 14 of Kahneman and Tversky’s gambles. These values are indicated in black

We can also search the parameter space for DFT parameters that are able to generate the highest likelihoods in their fits to Kahneman and Tversky’s choice data. We find that the best-fit values of θ for standard DFT and distracted DFT are 1.28 and 2.24 respectively, the best-fit values of α for standard DFT and distracted DFT are 0.75 and 0.46 respectively, and the best-fit value of π for distracted DFT is 0.74. Once again, the best-fit value of π is lower than 1, indicating that decision-makers are distracted when deliberating between Kahneman and Tversky’s (1979) gambles.

These estimations also yield a best-fit log-likelihood value of -594.35 for distracted DFT compared to a value of -714.95 for standard DFT¹¹. This is a significant difference using the likelihood-ratio test (p < 0.01). Additionally, the BIC value for standard DFT is 1,443.84, and the BIC value for distracted DFT is 1,209.61, indicating a better fit for distracted DFT. Note that both the log-likelihood ratios and the BIC ratios are higher in favor of distracted DFT for the model fits on Kahneman and Tversky’s (1979) data compared to Rieskamp’s (2008) data, indicating that distracted DFT provides a larger improvement over standard DFT for the former dataset. This is because Kahneman and Tversky’s (1979) data consists of the specific gambles and paradoxical choices that distracted DFT was generated to explain, whereas Rieskamp’s (2008) data consists of more general randomly generated gambles. The summary of model-fits for standard and distracted DFT on Kahneman and Tversky’s data is displayed in Table 2. Finally, Fig. 3 plots predicted choice probabilities from the best-fit DFT models against actual observed choice probabilities, for Kahneman and Tversky’s fourteen gambles. Actual observed choice probabilities are represented by plus signs, the predictions of standard DFT are represented by white circles, and the predictions of distracted DFT are represented by black squares.

Table 2 Summary of model fits to Kahneman and Tversky (1979). L corresponds to the best-fit log-likelihood of the model and BIC is the Bayes information criterion value for this fit. Note that π = 1 is fixed (and not-estimated) for standard DFT

Fig. 3

The choice probabilities predicted by best-fit standard DFT and distracted DFT, for Kahneman and Tversky’s (1979) gambles are plotted alongside actual observed choice probabilities for these gambles. These gambles are ordered in terms of increasing observed choice probability for gamble x

Discussion

Decision field theory is one of the best-known cognitive models of risky choice. It assumes that preferences are formed through the sequential sampling of possible events, with the attention towards the events equal to their occurrence probability. As a result of this, the direction of preference accumulation within DFT is determined by the relative expected utilities of the gambles in consideration, with preferences moving in favor of the gamble with the higher expected utility. This implies that the gamble with the higher expected utility is also the one that is the most likely to be selected. The relationship between modal choice and expected utility, posited by decision field theory, makes it unable to account for the common-ratio, common-consequence, reflection, and event-splitting effects, four important empirical findings in the domain of risky decision-making.

This paper has introduced a modification to decision field theory, that is capable of accounting for these effects. Particularly, it has assumed that event attention is vulnerable to stochastic error. With some probability π, decision-makers attend to events in accordance with their occurrence probability, but with some probability 1 − π, decision-makers get distracted, and attend to events uniformly. While the proposed stochastic error is not systematic, as every event is equally likely to be sampled when the decision-maker is distracted, it can nonetheless affect the direction of preference accumulation. Preferences do not necessarily accumulate in favor of the gamble with the highest expected utility, and additionally, changing various properties of the available gambles, while keeping the ranking of their expected utilities the same, can affect the direction of accumulation. This can reverse modal choice, and subsequently explain the common-ratio, common-consequence, reflection, and event-splitting effects.

The behaviors that this paper seeks to explain are some of the most important and robust results on preferential decision-making. They form a descriptive benchmark for any theory of risky choice. The fact that a minor extension to decision field theory can predict these behaviors, shows that these important results are within the descriptive scope of the sequential sampling and accumulation framework. Sequential sampling and accumulation is a popular approach to studying decision-making in psychology and neuroscience. It involves decision mechanisms that are neurally and cognitively feasible, and incorporating risky choice paradoxes within this framework yields valuable insights regarding the psychological substrates of risky choice. Note that current behavioral approaches to modeling these choices, such as cumulative prospect theory, involve a sequence of highly sophisticated mathematical steps; steps that are unlikely to be implemented successfully by human decision-makers.

In addition to specifying the psychological processes underlying preferential decision-making, incorporating the common-ratio, common-consequence, reflection, and event-splitting effects within the sequential sampling framework can yield valuable insights regarding the relationship of risky decision-making with behaviors in other psychological domains, such as perceptual and lexical choice. In fact, many key findings in these other domains have also been explained through stochastic error in sequential sampling models (see e.g. Ratcliff and Smith 2004 for a review). While error has a very different role in models of perceptual and lexical decision-making compared to distracted decision field theory (affecting, for example, starting points and accumulation strength instead of event attention), all of these models are similar in that they explain systematic behaviors using non-systematic stochastic noise. These similarities are especially striking when we contrast distracted DFT with existing explanations for the risky choice paradoxes, almost all of which are non-dynamic and deterministic.

The proposed distraction mechanism is highly simplified, but can be modified to incorporate other attentional biases. Instead of being described by a uniform distribution, as in this paper, distraction could be a function of event salience and vividness, due to exogenous contextual factors, or event accessibility, due to past experiences (Gonzalez et al. (2003); Loewenstein et al. 2001). This mechanism can also be interpreted in ways other than distraction. This paper has, for example, discussed the similarities and differences between the proposed distraction account of risky choice, and biased probability weighting as assumed in cumulative prospect theory and related approaches. While distraction differs from probability weighting in several important ways, it is nonetheless possible to interpret distraction as a psychological explanation for observed probability weighting biases in risky choice. Attention probabilities that depart from true event probabilities can also be seen as products of an exploration process, one in which decision-makers pay equal attention to all events while they familiarize themselves with gamble outcomes. Later in the decision, attention probabilities may begin to equal event probabilities, culminating in expected utility based accumulation. Such an interpretation would make novel predictions regarding the effect of factors such as speed stress on the magnitude of the above paradoxes. These are predictions that can be tested in futurework.

The proposed modification to decision field theory does not only predict modal choices for common-ratio, common-consequence, reflection and event-splitting gambles. It is also able to provide a powerful quantitative fit to Kahneman and Tversky’s (1979) dataset consisting of a large number of different choices made over these gambles. Additionally, a model comparison using Rieskamp’s (2008) choice data shows that distracted DFT also provides a good fit to choices involving randomly generated gambles. The assumption of stochastic error in event attention is thus necessary for both capturing the highly specific qualitative results regarding expected utility theory’s violations, and for improving the quantitative predictions of decision field theory in particular, and the sequential sampling framework in general.

Distracted decision field theory is also able to explain a number of additional risky behaviors. These include the possibility effect and the four-fold pattern, two paradoxes whose gambles are in fact included in the Kahneman and Tversky (1979) dataset that this model is fit on. Additionally, explaining risky choice paradoxes using decision field theory implies that other effects uniquely predicted by sequential sampling models are fully compatible with, and can emerge alongside, these risky choice paradoxes. These include findings involving decision times, time pressure, speed-accuracy tradeoffs, violations of independence between alternatives, serial position effects on preference, and violations of stochastic dominance with non-independent gambles (Busemeyer & Diederich 2002; Busemeyer & Townsend 1993; Diederich & Busemeyer 1999; Dror et al. 1999) Finally, the fact that the common-ratio, common-consequence, reflection, and event-splitting effects are easily accommodated within DFT implies that more subtle risky choice findings, such as stochastic dominance effects with event-splitting, violations of gain-loss separability, and violations of upper-tail independence and lower cumulative independence (see e.g. Birnbaum 2008) may also be predicted by this framework. While this paper has limited its focus to explaining the four main paradoxes of risky choice, future research can examine these additional findings, with the hope of generating a richer and more powerful cognitive theory of risky decision-making.