Search
Close
Search
Advanced Search
Search Menu

Abstract

The static and transient deformations produced by earthquakes cause density perturbations which, in turn, generate immediate, long-range perturbations of the Earth's gravity field. Here, an analytical solution is derived for gravity perturbations produced by a point double-couple source in homogeneous, infinite, non-self-gravitating elastic media. The solution features transient gravity perturbations that occur at any distance from the source between the rupture onset time and the arrival time of seismic P waves, which are of potential interest for real-time earthquake source studies and early warning. An analytical solution for such prompt gravity perturbations is presented in compact form. We show that it approximates adequately the prompt gravity perturbations generated by strike-slip and dip-slip finite fault ruptures in a half-space obtained by numerical simulations based on the spectral element method. Based on the analytical solution, we estimate that the observability of prompt gravity perturbations within 10 s after rupture onset by current instruments is severely challenged by the background microseism noise but may be achieved by high-precision gravity strainmeters currently under development. Our analytical results facilitate parametric studies of the expected prompt gravity signals that could be recorded by gravity strainmeters.

Transient deformation, Time variable gravity, Earthquake source observations, Theoretical seismology, Early warning

1 INTRODUCTION

Earthquakes generate transient and static deformation, including volumetric deformation and displacement of material interfaces, which modify the spatial distribution of material density. This mass redistribution induces changes in the Earth's gravitational field. Permanent gravity changes generated by static deformation induced by the co-seismic and post-seismic slip of large earthquakes have been observed by superconducting gravimeters and gravity field satellite missions on multiple occasions (Imanishi et al.2004; Wang et al.2012a; Fuchs et al.2013; Cambiotti & Sabadini 2013). Theoretical models of these static gravity perturbations have been developed (Okubo 1992; Sun et al.2009) and compared to observations (Matsuo & Heki 2011; Wang et al.2012b). The transient effects of elasto-gravitational coupling on the Earth's gravest normal modes are well established and routinely included in normal mode computations for long-period seismology (Dahlen & Tromp 1998). Transient perturbations of the gravity field concurrent with the passage of seismic waves have been examined as a broad-band source of so-called Newtonian noise for gravitational-wave (GW) detectors (Beker et al.2011; Driggers et al.2012). Here we address, for the first time, the problem of modelling the gravity perturbations generated by earthquakes at short timescales, including those generated by transient deformation induced by seismic waves and those occurring during the fault rupture.

Our focus here is on a particular short-term elasto-gravitational effect that has received no attention in the literature. Owing to the long-range and virtually instantaneous (speed-of-light) effect of gravitational forces, density perturbations lead immediately to global perturbations of the Earth's gravity field. In particular, the volumetric deformation carried by P waves induces remote gravity perturbations even at distances beyond the P-wave front. Hence, at any distance from an earthquake source and its dynamically deforming region, gravity perturbations are expected to be induced even between the onset time of the rupture and the arrival time of seismic waves. We refer to these as prompt gravity perturbations. If practically measurable, these signals would add a new dimension to real-time seismology that may enhance rapid earthquake source detection and parameter estimation capabilities and may contribute to earthquake and tsunami early warning. Some analogies may be drawn to prompt electromagnetic perturbations caused, in principle, by earthquakes via the electrokinetic effect in saturated porous media (Gao et al.2013) or via the motional induction effect of the Earth's conductive crust and magnetic field (Gao et al.2014). Here we develop building blocks for the quantitative analysis of prompt gravity perturbations, as needed to assess their detectability and information content. An analysis of their potential contribution to earthquake early warning will be reported elsewhere, as well as results of a search for prompt gravity signals in superconducting gravimeter recordings of a recent mega-earthquake.

While normal mode theory in global seismology accounts for gravitational effects (Takeuchi & Saito 1972; Dahlen & Tromp 1998), the structure of the prompt gravity perturbation field is not immediately evident from it. To facilitate systematic, parametric studies of transient gravity signals, we develop in Section 2 an analytical model of transient Newtonian gravity perturbations from point shear dislocations in unbounded, uniform, non-self-gravitating elastic media. The model accounts for the effects of density perturbations induced by both static and transient deformations and provides a complete gravity time-series, before and after the passage of seismic waves. The key result is a compact expression for prompt gravity perturbations. Its relevance in more realistic settings is assessed in Section 3 by comparing the analytical results with results from numerical simulations that include finite fault and free surface effects. In Section 4, after realizing that prompt gravity perturbations are generally too weak to be detected by conventional gravimeters within 10 s after rupture onset, we derive expressions for transient gravity gradients and assess the theoretical potential of high-sensitivity gravity strainmeters to observe prompt gravity signals.

2 GRAVITY PERTURBATIONS FROM POINT-SHEAR DISLOCATIONS IN INFINITE, HOMOGENEOUS, NON-SELF-GRAVITATING ELASTIC MEDIA

2.1 Model assumptions and density perturbations

We consider a point shear dislocation in an infinite, elastic and homogeneous medium. The deformation is related to the dislocation source by the seismic wave equation and the Newtonian gravity potential perturbation is related to the deformation-induced density perturbations by Poisson's equation. We ignore the effects of self-gravitation, that is we assume that gravity perturbations induced by deformation do not act back on the deformation and their contribution to the seismic wave equation is ignored. Self-gravitation effects are significant only at periods much longer than 100 s (see p. 142 of Dahlen & Tromp 1998), whereas our primary interest here is in the short timescales over which significant prompt gravity perturbations may develop (the P-wave traveltime from the hypocentre to distances of up to a few 100 km). We adopt a source-based coordinate system with origin at the location of the shear dislocation, z-axis parallel to the slip direction and x-axis perpendicular to the fault plane. Spherical coordinates r, θ, ϕ are related to the Cartesian coordinates via x = r sin (θ) cos (ϕ), y = r sin (θ)sin (ϕ), z = r cos (θ), with 0 < θ < π, and 0 < ϕ < 2π. The point-shear dislocation source is represented by a double-couple moment tensor point-source, with the following equivalent body-force:
\begin{eqnarray} \boldsymbol{f}(\boldsymbol{r},t) = -M_0(t)\left( \frac{\partial \delta (\boldsymbol{r})}{\partial z}\boldsymbol{e}_x + \frac{\partial \delta (\boldsymbol{r})}{\partial x}\boldsymbol{e}_z \right), \end{eqnarray}
(1)
where |$\boldsymbol{e}_x$| and |$\boldsymbol{e}_z$| are the unit vectors pointing along the corresponding coordinate axes. We assume a fixed focal mechanism but allow for an arbitrary seismic moment time function M0(t).
The displacement field induced by seismic waves is denoted by |$\boldsymbol{\xi }(\boldsymbol{r}\,,t)$|⁠. The resulting density perturbation |$\delta \rho (\boldsymbol{r}\,,t)$| is given by the linearized continuity equation (e.g. eq. 3.46 of Dahlen & Tromp 1998):
\begin{eqnarray} \delta \rho (\boldsymbol{r}\,,t) = -\rho _0\boldsymbol{\nabla }\cdot \boldsymbol{\xi }(\boldsymbol{r}\,,t) \end{eqnarray}
(2)
where ρ0 is the unperturbed mass density. It depends on the divergence of the displacement field, which describes volumetric deformations of the medium. From the known expression of the seismic wave field generated by a point double-couple source (Aki & Richards 2009):
\begin{eqnarray} \delta \rho (\boldsymbol{r}\,,t) = R_{\rm P}(\theta ,\phi )\ \Delta (r,t), \end{eqnarray}
(3)
where
\begin{eqnarray} R_{\rm P}(\theta ,\phi ) &=& \cos (\phi )\sin (2\theta )\nonumber \\ &=& 2(\boldsymbol{e}_x\cdot \boldsymbol{e}_r)(\boldsymbol{e}_z\cdot \boldsymbol{e}_r) \end{eqnarray}
(4)
is the quadrupolar P-wave radiation pattern, |$\boldsymbol{e}_r\equiv \boldsymbol{r}/r$| the radial unit vector, and
\begin{eqnarray} \Delta (r,t)&\equiv &\frac{3}{4\pi r^3\alpha ^2}\bigg (M_0(t-r/\alpha )\nonumber\\ &&+\,\frac{r}{\alpha }\dot{M}_0(t-r/\alpha )+\frac{r^2}{3\alpha ^2}\ddot{M}_0(t-r/\alpha )\bigg ) \end{eqnarray}
(5)
where α is the P-wave speed. Because S waves produce no volumetric deformation, density perturbations in infinite, uniform, elastic media are carried exclusively by P waves and hence depend on the moment time function delayed by the P-wave traveltime, M0(t − r/α). The density perturbation is plotted in Fig. 1 as a function of distance and time, for ϕ = 0 and θ = π/4. The plot shows that in addition to a lasting density change in the vicinity of the source, a propagating density perturbation is transported by the compressional waves.
Figure 1.
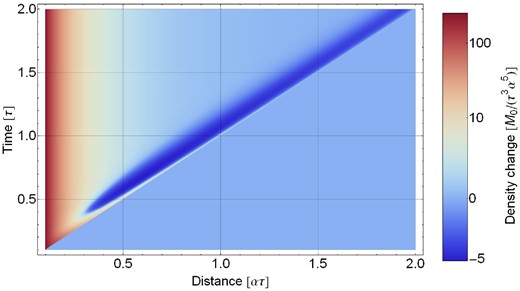
Density perturbation field as a function of distance and time, for ϕ = 0, θ = π/4 and seismic moment time function M0 tanh (t/τ)Θ(t), where Θ( · ) denotes the unit step function. Since the positive and negative values vary over many orders of magnitude, the colour scale is based on a log-modulus transformation (John & Draper 1980).
Open in new tabDownload slide

Density perturbation field as a function of distance and time, for ϕ = 0, θ = π/4 and seismic moment time function M0 tanh (t/τ)Θ(t), where Θ( · ) denotes the unit step function. Since the positive and negative values vary over many orders of magnitude, the colour scale is based on a log-modulus transformation (John & Draper 1980).

2.2 Prompt gravity perturbation

Prompt gravity perturbations are essentially the exterior gravitational field induced by the density perturbation outside its spatial support, that is, beyond the P-wave front. Their structure can be determined by exploiting classical results in potential theory (Jekeli 2007) as follows. The density perturbation field inherits the symmetries of a quadrupole from the P-wave radiation pattern, which features four lobes of alternating signs. A quadrupole density perturbation generates an exterior gravitational potential, which has also a quadrupole structure and decays as |$1/r_0^3$|⁠, where r0 is the distance to the centroid of the quadrupole.

In this section, we use seismic potentials (of the seismic fields and alternatively of the seismic sources) to obtain an explicit expression of the gravity perturbation in homogeneous space valid for all times. In the Appendix, a second method is described, which uses the spherical multipole expansion. While the method based on potentials is not very intuitive and does not give a direct interpretation of the effective source of gravity perturbations, it is more elegant and should prove useful also to solving more complicated calculations in the future, for example concerning gravity perturbations in a half space.

The perturbation of the Newtonian gravity potential, |$\delta \psi (\boldsymbol{r}_0\,,t)$|⁠, is determined by the density fluctuations according to Poisson's equation
\begin{eqnarray} \boldsymbol{\nabla }^2 \delta \psi = 4\pi G\delta \rho \end{eqnarray}
(6)
where G is the gravitational constant. In a uniform medium, the density perturbation is governed by the seismic displacement field via eq. (2). We represent the seismic field in terms of its Lamé potentials:
\begin{eqnarray} \boldsymbol{\xi }(\boldsymbol{r}\,,t)=\boldsymbol{\nabla }\phi _{\rm s}(\boldsymbol{r}\,,t)+\boldsymbol{\nabla }\times {\psi }_{\rm s}(\boldsymbol{r}\,,t). \end{eqnarray}
(7)
The scalar potential ϕs gives rise to compressional waves, whereas the vector potential |$\boldsymbol{\psi }_{\rm s}$| gives rise to shear waves and also obeys the condition |$\boldsymbol{\nabla }\cdot \boldsymbol{\psi }_{\rm s}=0$|⁠. Inserting eq. (7) into eq. (2) and noting that |$\boldsymbol{\nabla }\cdot \boldsymbol{\nabla }\times \boldsymbol{\psi }_{\rm s}=0$|⁠, one finds
\begin{eqnarray} \delta \rho = -\rho _0\boldsymbol{\nabla }^2 \phi _{\rm s} \end{eqnarray}
(8)
and, from eq. (6), |$\boldsymbol{\nabla }^2 \delta \psi = -4\pi G\rho _0\boldsymbol{\nabla }^2\phi _{\rm s}$|⁠. Hence, considering the anticipated fast (⁠|$1/r_0^3$|⁠) decay of the gravity potential away from the density perturbation region, one finds for an infinite medium
\begin{eqnarray} \delta \psi (\boldsymbol{r}_0\,,t)=-4\pi G\rho _0\phi _{\rm s}(\boldsymbol{r}_0\,,t). \end{eqnarray}
(9)
This equivalence between a potential giving rise to a seismic compressional field and the corresponding gravity potential perturbation is remarkable. Given the known solution for seismic potentials from a point force in infinite media (Aki & Richards 2009), one can derive the expression for a double-couple and rescale it according to eq. (9) to obtain the following expression of the perturbed gravity potential:
\begin{eqnarray} \delta \psi (\boldsymbol{r}_0\,,t)&=& G R_{\rm P}(\theta _0,\phi _0)\nonumber\\ &&\!\times \bigg [\frac{1}{r_0\alpha ^2}M_0(t-r_0/\alpha )-\frac{3}{r_0^3}\int \limits _0^{r_0/\alpha }\!\!{\rm d} u\,u M_0(t-u)\bigg ]. \end{eqnarray}
(10)
Note that this result does not depend explicitly on the reference density of the medium. Before the arrival of P waves, when t < r0/α, the first term in brackets vanishes, the upper limit of integration of the second term can be substituted by t, and
\begin{eqnarray} \int \limits _0^t{\rm d} u\,u M_0(t-u)= \int \limits _0^t{\rm d} t^{\prime }\int \limits _0^{t^{\prime }}{\rm d}t^{\prime \prime } M_0(t^{\prime \prime }) \equiv I_2[M_0](t) \end{eqnarray}
(11)
if M0(t) = 0 for t < 0. Therefore, the early gravity potential assumes a remarkably simple form independent of the speed α of compressional waves:
\begin{eqnarray} \delta \psi (\boldsymbol{r}_0\,,t)=- R_{\rm P}(\theta _0,\phi _0)\frac{3G}{r_0^3}I_2[M_0](t). \end{eqnarray}
(12)
As anticipated, the prompt gravity potential inherits the quadrupole distribution of the P-wave radiation pattern and decays as |$1/r_0^3$|⁠. Its relation to the seismic moment is remarkably simple: it is proportional to the second integral of the seismic moment time function.

The derivation, in particular eq. (9), has the unintuitive feature that the prompt gravity potential perturbation appears to emerge from the ‘acausal’ component of the P-wave potential. This component has actually no physical significance in the seismic wave equation, where its contribution to the near-field seismic wavefield is cancelled out by a similar contribution from the S-wave potential.

We can provide an alternative derivation of the prompt gravity potential perturbation based on source potentials, which allows further insight into the origin of its simple structure. Taking the second time derivative of eq. (9) and considering the wave equation for the P-wave potential,
\begin{eqnarray} \ddot{\phi }_{\rm s} = \alpha ^2 \boldsymbol{\nabla }^2 \phi _{\rm s} + \Phi /\rho _0, \end{eqnarray}
(13)
where |$\Phi (\boldsymbol{r},t)$| is the scalar Helmholtz potential of the equivalent body force representation of a dislocation (e.g. eq. 4.9 of Aki & Richards 2009), we find
\begin{eqnarray} \delta \ddot{\psi }= -4\pi G\rho _0 ( \alpha ^2 \boldsymbol{\nabla }^2 \phi _{\rm s} + \Phi /\rho _0 ). \end{eqnarray}
(14)
Making use of eq. (8), we get
\begin{eqnarray} \delta \ddot{\psi }= -4\pi G (-\alpha ^2\delta \rho + \Phi ) . \end{eqnarray}
(15)
The first term in brackets is a propagative contribution carried by P waves. The second term is long-ranged. Before the arrival of P waves to the detector, only the second term is non-zero and hence the prompt gravity potential perturbation satisfies
\begin{eqnarray} \delta \ddot{\psi }= -4\pi G \Phi . \end{eqnarray}
(16)
Combining spatial derivatives of the point-force potential given, for example, in eq. (4.17) of Aki & Richards (2009), it can be shown that the scalar Helmholtz potential of the double-couple source given in eq. (1) is
\begin{eqnarray} \Phi (\boldsymbol{r},t) = \frac{M_0(t)}{2\pi } \frac{\partial ^2 1/r}{\partial x \partial z}. \end{eqnarray}
(17)
Porting this into eq. (16) and integrating twice lead to eq. (12). This derivation, in particular eq. (16), provides a more elegant proof that the prompt gravity potential perturbation is proportional to the second integral of M0(t). Also, eq. (15) is consistent with eq. (10) but shows more clearly the separation between propagative and long-ranged components of the gravity potential field.
Finally, we provide an explicit expression of the prompt perturbation of gravity acceleration, |$\delta \boldsymbol{a} = -\nabla \delta \psi$|⁠, which takes the form
\begin{eqnarray} \delta \boldsymbol{a}(\boldsymbol{r}_0\,,t)&=& \frac{6G}{r_0^4}((\boldsymbol{e}_z\cdot \boldsymbol{e}_r)\boldsymbol{e}_x +(\boldsymbol{e}_x\cdot \boldsymbol{e}_r)\boldsymbol{e}_z\nonumber \\ && -\,5(\boldsymbol{e}_x\cdot \boldsymbol{e}_r)(\boldsymbol{e}_z\cdot \boldsymbol{e}_r)\boldsymbol{e}_r) I_2[M_0](t). \end{eqnarray}
(18)
Reflecting the long-range and instantaneous nature of gravity changes, these expressions show that the prompt gravity perturbation extends over arbitrary distances and involves the seismic moment time-function without P-wave time delay. Its proportionality to the second integral of seismic moment has important implications. Compared to far-field seismic ground displacements, which are proportional to seismic moment rate, the high-frequency content of prompt gravity potential perturbations is damped. For self-similar ruptures, whose moment function has an onset proportional to t3, the prompt gravity potential signal is predicted to start as t5. After the rupture ends and before the P wave arrives, it grows as t2. At the arrival of P waves, t = r0/α and |$\delta \boldsymbol{a} \propto t^2/r_0^4 \propto 1/r_0^2$|⁠, consistent with the distance decay of gravity perturbations produced by static earthquake deformation (Okubo 1991). In the calculations leading to eq. (12), it is found that the near-, intermediate- and far-field terms of the density perturbation, represented by the three terms in eq. (5), have comparable contributions to the prompt gravity perturbation. In particular, the contribution of the static deformation (the near-field term) is not dominant at any distance.

3 COMPARISON WITH SPECTRAL ELEMENT SIMULATIONS

The theory developed in Section 2 does not capture all effects that may be present in nature. Even if for some purposes the Earth can be sufficiently approximated by a homogenous medium, it remains to be determined under which conditions this theory adequately describes finite fault sources in a half space.

First, the theoretical results are derived for a point source. Additional finite-source effects are expected close to a finite-size rupture. We do not consider this a major drawback, since the problem is linear and finite-sized sources of arbitrary shape and with complicated rupture propagation can be represented by superposition of point sources. A suitable approximation to describe finite-size ruptures on a single planar fault is proposed here. The prompt gravity perturbation in that scenario is a superposition of quadrupole gravity fields, each of the form given by eq. (12). The leading term of the multipole expansion of a superposition of quadrupoles is also a quadrupole, whose quadrupole moment is simply the sum of the individual ones. The higher order multipole terms (octupole, etc.) are not necessarily zero but they decay faster with distance. Hence, at a distance from the P-wave front, the prompt gravity perturbation produced by a finite earthquake source is approximately given by eq. (12) if, as conventionally in seismology, M0(t) is understood as the seismic moment integrated over the whole finite rupture surface. To minimize the octupole contribution, r0 should be understood as the distance to the instantaneous earthquake centroid (or, more generally, to the instantaneous centroid of the density perturbation field). The quality of this approximation is expected to degrade as the P-wave front approaches.

Secondly, the analytical solution was derived for infinite media. If an event occurs at a depth h, then we can expect deviations from our results as soon as P waves reach the surface at time h/α, which is typically a few seconds only. Therefore, simulating many tens of seconds of gravity time-series using the analytical results of Section 2 would in general lead to inaccurate predictions. However, for early warning applications of prompt gravity signals the important question is if the influence of the surface is significant within a few seconds of the rupture onset.

Finite-source and free-surface effects can be assessed by comparing the analytical prediction with results obtained from a numerical simulation on a half-space. The simulation tool used here is SPECFEM3D, a seismic wave propagation code based on the spectral element method (Komatitsch & Vilotte 1998; Komatitsch & Tromp 1999) which can simulate finite earthquake sources with prescribed slip rate (S. N. Somala, J.-P. Ampuero and N. Lapusta, Finite-fault source inversion using adjoint methods in 3D heterogeneous media, submitted). We implemented in SPECFEM3D the computation of gravity acceleration perturbations above the half-space surface produced by the seismic displacement field |$\boldsymbol{\xi }(\boldsymbol{r}\,,t)$| as a function of time, based on the following equation [Harms et al. (2009); eqs 3.100–3.101 of Dahlen & Tromp (1998)],
\begin{eqnarray} \delta \boldsymbol{a}(\boldsymbol{r}_0,t) = G\rho _0\int {\rm d} V\frac{1}{|\boldsymbol{r}-\boldsymbol{r}_0|^3}\left(\boldsymbol{\xi }(\boldsymbol{r}\,,t) -3(\boldsymbol{e}_r\cdot \boldsymbol{\xi }(\boldsymbol{r}\,,t))\cdot \boldsymbol{e}_r\right).\nonumber \\ \end{eqnarray}
(19)
This equation has the form of a dipole perturbation associated with displaced point masses ρ0 dV. It is valid as long as the displacement is much smaller than the distance |$|\boldsymbol{r}-\boldsymbol{r}_0|$|⁠. The integral is performed over a fixed domain but it accounts for the gravity perturbations induced by deformation of the Earth's surface. Eq. (19) gives the Eulerian gravity acceleration measurable by a seismically isolated sensor, whereas the Lagrangian quantity measured by a non-isolated sensor involves an additional term representing advection through the initial gravity gradient (Dahlen & Tromp 1998). This distinction is, however, irrelevant before seismic waves arrive to the sensor. In this section, we compare the simulated half-space gravity perturbation with the full-space analytical solution of prompt gravity acceleration perturbations, eq. (18).

The assumed kinematic source model is specified in Appendix B. It represents a circular pulse-like rupture of finite duration τ with cosine slip rate function, uniform final slip δ, rise time T and constant rupture speed vrup. From the rupture model, an explicit expression of the moment function M0(t) is obtained that is inserted into eq. (18) to calculate an analytical prediction of the gravity perturbation. We present results of three simulations, a very deep strike-slip event, a shallow one and a shallow dip-slip event, and compare them with the analytical predictions. The duration of the strike-slip events is τ = 2 s, while the duration of the dip-slip event is 4 s. The rise time in all cases is T = 1 s. We simulated about 5 s of time-series, a short timescale relevant to anticipated applications in early warning. It is computationally expensive to increase the simulation duration and at the same time increase the size of the simulation domain to encompass the complete P-wave front and preserve accuracy at high frequencies. Further parameter values of the simulations are listed in Table 1. For the strike-slip scenarios, the total ruptured area is A = π(vrupτ)2 and the seismic moment M0 = μδA. In the dip-slip scenario the rupture reaches the surface.

Table 1.

Parameter values used for the comparison between the numerical simulation and theory.

ParameterSymbolValue
Rupture speedvrup3 km s−1
P-wave speedα6.4 km s−1
Mass densityρ02670 kg m−3
Shear modulusμ27 GPa
Slipδ0.5 m
Strike-slip events
Total ruptured areaA110 km2
Total seismic momentM01.5 × 1018 N m
Moment magnitudeMw6.1
Dip-slip event
Total ruptured areaA400 km2
Total seismic momentM05.4 × 1018 N m
Moment magnitudeMw6.5
ParameterSymbolValue
Rupture speedvrup3 km s−1
P-wave speedα6.4 km s−1
Mass densityρ02670 kg m−3
Shear modulusμ27 GPa
Slipδ0.5 m
Strike-slip events
Total ruptured areaA110 km2
Total seismic momentM01.5 × 1018 N m
Moment magnitudeMw6.1
Dip-slip event
Total ruptured areaA400 km2
Total seismic momentM05.4 × 1018 N m
Moment magnitudeMw6.5
Open in new tab
Table 1.

Parameter values used for the comparison between the numerical simulation and theory.

ParameterSymbolValue
Rupture speedvrup3 km s−1
P-wave speedα6.4 km s−1
Mass densityρ02670 kg m−3
Shear modulusμ27 GPa
Slipδ0.5 m
Strike-slip events
Total ruptured areaA110 km2
Total seismic momentM01.5 × 1018 N m
Moment magnitudeMw6.1
Dip-slip event
Total ruptured areaA400 km2
Total seismic momentM05.4 × 1018 N m
Moment magnitudeMw6.5
ParameterSymbolValue
Rupture speedvrup3 km s−1
P-wave speedα6.4 km s−1
Mass densityρ02670 kg m−3
Shear modulusμ27 GPa
Slipδ0.5 m
Strike-slip events
Total ruptured areaA110 km2
Total seismic momentM01.5 × 1018 N m
Moment magnitudeMw6.1
Dip-slip event
Total ruptured areaA400 km2
Total seismic momentM05.4 × 1018 N m
Moment magnitudeMw6.5
Open in new tab

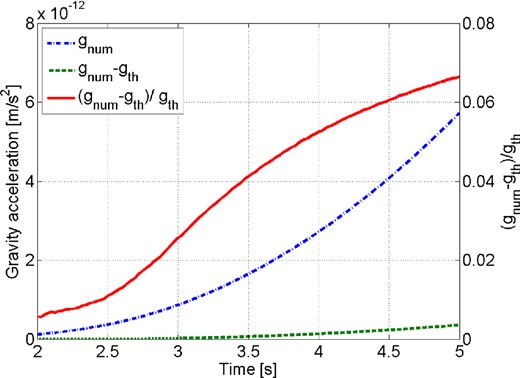
Fig. 2 shows the comparison between theory and simulation for the deep strike-slip event with hypocentre at 50 km depth. We compare the gravity acceleration in the horizontal direction normal to the fault evaluated at a horizontal distance of 1 km to the epicentre and to the fault (to avoid a null of gravity acceleration) and 2 km above ground (to avoid exponentially decaying artefacts of the gravity calculation related to the finite grid density). The relative deviation (shown as dashed line) grows with time but stays smaller than 7 per cent over the entire 5 s. This serves as verification of our SPECFEM3D implementation and to show that finite source effects are not significant at this distance.

Figure 2.
Comparison between analytical predictions gth and numerical simulation gnum of prompt gravity acceleration perturbations for a deep strike-slip earthquake. The solid curve is plotted against the right y-axis, while the dashed and dash-dotted curves are plotted against the left y-axis. The hypocentre is 50 km deep so that surface effects are non-existent during the first 5 s. The detector is located at a horizontal distance of 1 km from the epicentre to avoid a null of gravity acceleration. The result shows that approximating the fault rupture as a point source leads to relative deviations smaller than 0.07 within the first 5 s.
Open in new tabDownload slide

Comparison between analytical predictions gth and numerical simulation gnum of prompt gravity acceleration perturbations for a deep strike-slip earthquake. The solid curve is plotted against the right y-axis, while the dashed and dash-dotted curves are plotted against the left y-axis. The hypocentre is 50 km deep so that surface effects are non-existent during the first 5 s. The detector is located at a horizontal distance of 1 km from the epicentre to avoid a null of gravity acceleration. The result shows that approximating the fault rupture as a point source leads to relative deviations smaller than 0.07 within the first 5 s.

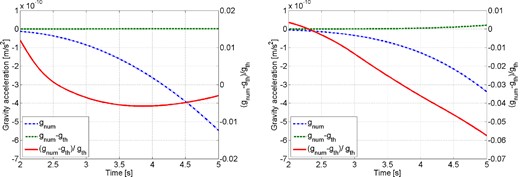
Fig. 3 (left) shows the comparison for the shallow strike-slip event with hypocentre depth 7.5 km. Gravity is evaluated at 50 km horizontal distance to the epicentre and 2 km above ground. The horizontal distance was chosen larger than the propagation distance of seismic waves during the first 5 s. The plot in the right of Fig. 3 shows the comparison for the 7.5 km deep dip-slip event with 45° dip angle, and 4 s duration. In these two examples, the relative deviation is smaller than 1.5 and 6 per cent, respectively. This is even smaller than in the previous example, which may seem surprising given that at t = 5 s seismic waves have already been reflected from the surface or have been converted into surface waves, which was not considered in the theoretical analysis. Especially concerning the dip-slip event, one might have expected more significant deviations since the surface experiences a differential lift across the fault trace when the rupture reaches the surface at about t = 3.5 s. The agreement between the theoretical and numerical results even in this case may be taken as a hint of a more fundamental principle that is to be discovered in the full half-space solution.

Figure 3.
Comparison between analytical predictions gth and numerical simulation gnum of prompt gravity acceleration perturbations for a shallow strike-slip earthquake and a surface-breaking dip-slip earthquake. Same representation as in Fig. 2. Left: strike-slip event with 2 s duration. Right: dip-slip event with dip angle of 45° and duration of 4 s. In both cases, the event hypocentre is 7.5 km deep so that surface effects can be expected shortly after 1 s, and the detector is located at 50 km distance from the epicentre so that seismic waves do not reach it within the 5 s of simulation time. For the dip-slip scenario, the rupture reaches the surface at about 3.5 s. The impact of the surface onto gravity perturbations stays weak within the first 5 s, leading to relative deviations smaller than 0.015 for the strike-slip event, and 0.06 for the dip-slip event.
Open in new tabDownload slide

Comparison between analytical predictions gth and numerical simulation gnum of prompt gravity acceleration perturbations for a shallow strike-slip earthquake and a surface-breaking dip-slip earthquake. Same representation as in Fig. 2. Left: strike-slip event with 2 s duration. Right: dip-slip event with dip angle of 45° and duration of 4 s. In both cases, the event hypocentre is 7.5 km deep so that surface effects can be expected shortly after 1 s, and the detector is located at 50 km distance from the epicentre so that seismic waves do not reach it within the 5 s of simulation time. For the dip-slip scenario, the rupture reaches the surface at about 3.5 s. The impact of the surface onto gravity perturbations stays weak within the first 5 s, leading to relative deviations smaller than 0.015 for the strike-slip event, and 0.06 for the dip-slip event.

Strong deviations between theory and numerical simulations were only observed for shallow events in cases where gravity was evaluated close to the epicentre so that the contribution from passing Rayleigh waves was dominant. An open question that should be addressed in future studies is whether results still agree well even long after 5 s, at least as long as contributions from passing Rayleigh waves can be excluded. The effect of heterogeneity of the crust also deserves further scrutiny.

4 TRANSIENT GRAVITY GRADIENTS

4.1 Motivations

Prompt gravity perturbations produced by earthquakes have not been observed with existing gravimeters or seismometers. An order-of-magnitude estimate of the amplitude of the prompt gravity acceleration signal can be obtained from eq. (18), neglecting the dependence on directions. We assume a self-similar rupture model, whose seismic moment function starts as M0(t) ∼ t3. Based on empirical relations between seismic moment and rupture duration (Houston 2001) we set M0(1 s) = 1017 N m. We find that
\begin{eqnarray} \delta a = O(10^6\,{\rm m^5 s^{-7}}) \frac{t^5}{r_0^4} \sim O(10\,{\rm nm/s}^2) \frac{(t/10\,{\rm s})^5}{(r_0/50\,{\rm km})^4} \end{eqnarray}
(20)
with t < r0/α (before the P-wave arrival). Note that 50 km is the typical distance travelled by a P wave in 10 s. This estimate is only valid before the half-duration of the rupture; after that it overestimates the signal amplitude. At late times, if the rupture duration and distance are large enough, prompt gravity perturbations above 10 nm s−2 are predicted. However, gravity acceleration changes forming within the first few seconds at local distances to the source (50 km or less) lie well below 10 nm s−2. This is also illustrated in the figures in Section 3. Measurements of such weak gravity transients are masked by a foreground of seismic noise (Berger et al.2004; Brown et al.2014), which is of the order of 100 nm s−2 between 0.1 Hz and 1 Hz. A novel class of instruments, for example seismically isolated gravity gradiometers (also referred to as gravity strainmeters (Harms et al.2013)), is required to detect these early transients.

The past two decades have seen rapid progress in the development of ultra-sensitive gravity strainmeters, mainly driven by scientific communities working on GW detection from astrophysical sources. Gravity strain is the relative change in physical distance between two test masses in response to a changing gravitational field. This change can be produced by a GW of astrophysical origin as well as by gravity perturbations from terrestrial sources. Laser-interferometric GW detectors such as LIGO (LIGO Scientific Collaboration 2009), Virgo (Accadia et al.2011), GEO600 (Lück et al.2010), and KAGRA (Aso et al.2013) measure gravity strain as differential displacement between seismically isolated test masses using high-power, in-vacuum lasers. Strain sensitivities of better than 10− 22 Hz− 1/2 have been demonstrated in the frequency range between about 50 and 1000 Hz. The LIGO and Virgo detectors are currently being upgraded to advanced configurations with design strain sensitivity better than 10− 23 Hz− 1/2 between about 30 Hz and 2000 Hz. Furthermore, future ground-based detectors have been proposed, such as the Einstein Telescope (ET Science Team 2011) with even more enhanced strain sensitivity, and a detection band extending down to a few Hz. In parallel to these kilometre-scale detectors, groups are developing gravity strainmeters targeting signals below 1 Hz, which are better suited to detect gravity perturbations changing over timescales of a few seconds (Ando et al.2010; Hohensee et al.2011; Dickerson et al.2013; Shoda et al.2014).

In the next section, we derive expressions for gravity strain perturbations (expressed as gravity gradients, i.e. the second time derivative of gravity strain) useful to assess the capability of future sensors to observe prompt gravity signals. Current concepts and sensitivity goals of these ‘low-frequency’ instruments are briefly reviewed in Section 4.4.

4.2 Gravity-gradient tensor

The gravity-gradient tensor is given by
\begin{eqnarray} {\mathsf {D}}(\boldsymbol{r}_0\,,t) =\boldsymbol{\nabla }\delta \boldsymbol{a}(\boldsymbol{r}_0\,,t) =-(\boldsymbol{\nabla }\otimes \boldsymbol{\nabla })\delta \psi (\boldsymbol{r}_0\,,t) \end{eqnarray}
(21)
where ‘⊗’ denotes the Kronecker product (also known as dyadic or tensor product). It is a symmetric tensor. Substituting eq. (10) for the gravity potential, one obtains a tensor that can be divided into four parts, distinguished by their dependence on directions. The first part is proportional to the local density perturbation:
\begin{eqnarray} {\mathsf {D}}_1(\boldsymbol{r}_0\,,t)=-4\pi G\,\delta \rho (\boldsymbol{r}_0\,,t)\boldsymbol{e}_r\otimes \boldsymbol{e}_r. \end{eqnarray}
(22)
It is the only contribution with non-vanishing trace. Using |${\rm Tr}(\boldsymbol{a}\otimes \boldsymbol{b}\,)=\boldsymbol{a}\cdot \boldsymbol{b}$|⁠, one obtains
\begin{eqnarray} {\rm Tr}({\mathsf {D}}_1(\boldsymbol{r}_0,t))=-4\pi G\,\delta \rho (\boldsymbol{r}_0,t), \end{eqnarray}
(23)
consistent with Poisson's equation. The second part can be cast into the form
\begin{eqnarray} {\mathsf {D}}_2 (\boldsymbol{r}_0\,,t) = -\frac{6 G}{r_0^5}\ \mathbf {S}(\theta ,\phi )\ \int \limits _0^{r_0/\alpha }{\rm d} u\,u M_0(t-u) \end{eqnarray}
(24)
where
\begin{eqnarray} \mathbf {S}(\theta ,\phi ) &=& 5(\boldsymbol{e}_x\cdot \boldsymbol{e}_r)(\boldsymbol{e}_z\cdot \boldsymbol{e}_r)(3 \,\, {1} \,\, -7\boldsymbol{e}_r\otimes \boldsymbol{e}_r) + \, 4(\boldsymbol{e}_x\otimes \boldsymbol{e}_z)_{\rm sym}+5((\boldsymbol{e}_x\times \boldsymbol{e}_r)\otimes (\boldsymbol{e}_z\times \boldsymbol{e}_r))_{\rm sym}. \end{eqnarray}
(25)
Here |$(\boldsymbol{a}\otimes \boldsymbol{b})_{\rm sym}\equiv \boldsymbol{a}\otimes \boldsymbol{b}+\boldsymbol{b}\otimes \boldsymbol{a}$|⁠. The third part is given by
\begin{eqnarray} {\mathsf {D}}_3(\boldsymbol{r}_0\,,t) &=& \frac{2 G}{5 r_0^3\alpha ^2}\left(6M_0(t-r_0/\alpha )+\frac{r_0}{\alpha }\dot{M}_0(t-r_0/\alpha )\right)\nonumber\\ &&\cdot \left(\mathbf {S}(\theta ,\phi )+(\boldsymbol{e}_x\otimes \boldsymbol{e}_z)_{\rm sym}\right), \end{eqnarray}
(26)
and the last part is proportional to the delayed moment function
\begin{eqnarray} {\mathsf {D}}_4(\boldsymbol{r}_0\,,t)=-\frac{2 G}{\alpha ^2r_0^3} M_0(t-r_0/\alpha ) \cdot (\boldsymbol{e}_x\otimes \boldsymbol{e}_z)_{\rm sym}, \end{eqnarray}
(27)
Note that the unit vectors |$\boldsymbol{e}_x$| and |$\boldsymbol{e}_z$| are not arbitrary coordinate axes, but correspond to the fault normal and slip direction. The full gravity-gradient tensor is simply the sum of these four contributions. For small times relevant to prompt perturbations, t < r0/α, the first and last two contributions vanish since M0(t) = 0 for t < 0, and the integral of the second contribution can be rewritten as
\begin{eqnarray} {\mathsf {D}} (\boldsymbol{r}_0\,,t)= -\frac{6 G}{r_0^5}\ \mathbf {S}(\theta ,\phi )\ I_2[M_0](t). \end{eqnarray}
(28)
None of the four contributions vanishes for t → ∞. Instead the time derivatives of the moment function go to zero, and the moment function itself can be substituted by its final value M0(t → ∞). The result is a gravity-gradient tensor whose components decrease with |$1/r_0^3$|⁠, and is consistent with the static gravity perturbation found by Okubo (1991) for shear dislocations in a half space, provided that his result is evaluated for an event far from the surface.

4.3 Gravity-strain response

The instruments anticipated to observe weak gravity transients of the form given in eq. (28) measure changes in distance between test masses or relative rotations between suspended bars. These instruments measure the so-called gravity-strain tensor|${\mathsf {h}}\equiv I_2[{\mathsf {D}}](t)$|⁠, rather than the gravity-gradient tensor |${\mathsf {D}}$|⁠. The concept of gravity strain is similar to that of elastic strain. While elastic strain determines the relative change in distance between test masses bolted to an elastic medium, gravity strain causes a relative change in distance between freely falling test masses. The concept of gravity strain is predominantly used in the GW community, and since it emerged from studies of gravity in the framework of general relativity, it should also be emphasized that some of the predicted effects on instruments cannot be explained by Newtonian gravity theory. Nonetheless, in the context of this paper, it is sufficient to understand gravity strain as if produced by a tidal force and therefore it can be calculated from the gravity-gradient tensor by double integration as stated above.

There are two types of gravity strain measurements: (1) the conventional scheme, which is a measurement of the relative displacement of test masses typically carried out along two perpendicular baselines (arms); and (2) measurement of the relative rotation between two suspended bars. In either case, the response of a sensor is obtained by projecting the gravity strain tensor onto a combination of two unit vectors, |$\boldsymbol{e}_1$| and |$\boldsymbol{e}_2$|⁠, that characterize the orientation of the detector, such as the directions of the two bars in a rotational gravity strainmeter, or the two arms of a conventional gravity strainmeter. This requires us to define two different gravity strain projections. The projection for the rotational strain measurement is given by
\begin{eqnarray} h_\times (\boldsymbol{r}_0\,,t)=\left(\boldsymbol{e}_1^{\top }\cdot {\mathsf {h}}(\boldsymbol{r}_0\,,t)\cdot \boldsymbol{e}_1^{\,\rm r}-\boldsymbol{e}_2^{\top }\cdot {\mathsf {h}}(\boldsymbol{r}_0\,,t)\cdot \boldsymbol{e}_2^{\,\rm r}\right)\!/2, \end{eqnarray}
(29)
where the subscript × indicates that the response to gravity fields is based on a relative rotation of the bars. The vectors |$\boldsymbol{e}_1^{\,\rm r}$| and |$\boldsymbol{e}_2^{\,\rm r}$| are rotated counter-clockwise by 90° with respect to |$\boldsymbol{e}_1$| and |$\boldsymbol{e}_2$|⁠. In the case of perpendicular bars |$\boldsymbol{e}_1^{\,\rm r}=\boldsymbol{e}_2$| and |$\boldsymbol{e}_2^{\,\rm r}=-\boldsymbol{e}_1$|⁠. The corresponding projection for the conventional gravity strainmeter reads
\begin{eqnarray} h_+(\boldsymbol{r}_0\,,t)=\left(\boldsymbol{e}_1^{\top }\cdot {\mathsf {h}}(\boldsymbol{r}_0\,,t)\cdot \boldsymbol{e}_1-\boldsymbol{e}_2^{\top }\cdot {\mathsf {h}}(\boldsymbol{r}_0\,,t)\cdot \boldsymbol{e}_2\right)\!/2. \end{eqnarray}
(30)
The subscript + indicates that the response is based on a distance change between test masses. It is straightforward to evaluate the projections of the strain tensor in the form given in equations (22), (24), (26) and (27) using the relation |$\boldsymbol{e}_1^\top \cdot (\boldsymbol{a}\otimes \boldsymbol{b})\cdot \boldsymbol{e}_2=$||$(\boldsymbol{e}_1\cdot \boldsymbol{a})(\boldsymbol{e}_2\cdot \boldsymbol{b})$|⁠.
Transformations between coordinate systems governed by a rotation matrix R can be applied to the strain tensor in the usual way
\begin{eqnarray} {\mathsf {h}}^{\prime }(\boldsymbol{r}_0^{\prime }\,,t)= R^\top \cdot {\mathsf {h}}(\boldsymbol{r}_0\,,t)\cdot R, \end{eqnarray}
(31)
and the projection is now carried out expressing the unit vectors in the transformed coordinates. This transformation can also be interpreted as a real rotation of the detector frame representing a change in detector orientation. For the case of perpendicular bars or arms of the gravity strainmeter, we calculate the detector response to gravity strain before the arrival of P waves, as given in eq. (28). Denoting the square-root of the average of the squared strain amplitude over detector orientations (represented by the frame rotations R), fault orientation, and slip direction by 〈 · 〉, one obtains:
\begin{eqnarray} \langle h_+(\boldsymbol{r}_0\,,t)\rangle =\langle h_\times (\boldsymbol{r}_0\,,t)\rangle =\frac{6\sqrt{14/5}\,G}{r_0^5} I_4[M_0](t), \end{eqnarray}
(32)
where I4 is the forth time integral. This expression allows us to make simple evaluations of expected gravity strain signal amplitudes without having to specify directions and orientations. Adopting similar assumptions as in Section 4.1, we derive the following order-of-magnitude estimate of the amplitude of prompt gravity strain signals:
\begin{eqnarray} \langle h \rangle \sim 6\ 10^4\,{\rm m^5\,s^{-7}}\ \frac{t^7}{r_0^5} \sim 10^{-12} \frac{(t/10\, {\rm s})^7}{(r_0/ 50\, {\rm km})^5}. \end{eqnarray}
(33)
As explained in the following section, there are at least three detector concepts that can reach these sensitivities.

4.4 Sensitivity of low-frequency gravity strainmeters

We conclude with a brief discussion about instruments and instrumental concepts potentially able to detect the gravity transients from earthquakes discussed in this work. Several concepts have been proposed for gravity strainmeters that target signals between 10 mHz and 10 Hz. These include atom-interferometric, laser-interferometric, torsion-bar, and superconducting gravity strainmeters (Moody et al.2002; Harms et al.2013). While none of the concepts has reached the sensitivity yet required for the detection of earthquake transients, sensitivities of 10−15 Hz−1/2 in the region 0.1–1 Hz seem within reach. Correspondingly and according to eq. (33), transient gravity signals from earthquakes at ∼10 s after rupture onset and at epicentral distances ∼50 km can be expected to have high signal-to-noise ratio. We point out that these low-frequency strainmeters are much smaller scale (of the order of 1 to 10 m) than the km-scale GW detectors LIGO and Virgo, which operate at higher frequencies. In fact, some of the modern concepts of low-frequency gravity strainmeters evolved from well-known gravity gradiometer technology. We also want to emphasize that the sensitivity of low-frequency gravity strainmeters required for the detection of earthquake transients lies well below the sensitivity required for GW detection at the same frequencies, which is about 10−19 Hz−1/2 at 0.1 Hz (Harms et al.2013). So it is conceivable that these instruments can be either early prototypes of future GW detectors, or instruments specifically built for geophysical observations.

Groups working on the realization of these new concepts rely on modern understanding of terrestrial gravity noise, seismic isolation, and thermal noise acquired over the past decade. For seismic-noise suppression, each concept follows a different strategy. Atom-interferometric detectors use freely falling ultracold atom clouds, and seismic noise couples strongly suppressed into the system through the laser interacting with the atoms (Baker & Thorpe 2012). Superconducting gravity strainmeters achieve seismic-noise reduction by common-mode suppression by differential readout of test-mass displacements versus a common rigid reference (Moody et al.2002). Laser-interferometric concepts rely on active and passive seismic isolation of suspended test masses (Harms et al.2013). Torsion-bar detectors profit from the mechanical filtering of seismic noise through a potentially very low frequency torsion resonance (Ando et al.2001). In reality, isolation performance is impeded by cross-coupling between degrees of freedom allowing seismic noise to couple into the strainmeter output through unwanted channels. The goal is to improve the mechanical designs to suppress these couplings.

As explained by Harms et al. (2013), terrestrial gravity noise is expected to pose sensitivity limitations at a level 10−15 Hz−1/2 at 0.1 Hz mainly due to atmospheric infrasound, and possibly also seismic fields (depending on the instrument site). It was proposed to use microphone or seismometer arrays to coherently cancel associated gravity fluctuations from the strainmeter data. However, this technique is mostly unexplored and therefore its performance is difficult to predict. Some experience has been gained with the cancellation of atmospheric gravity noise in gravimeter data (Neumeyer 2010), but gravity-noise cancellation in gravity gradiometers is not equivalent to cancellation in gravimeters.

The best strain sensitivity at 0.1 Hz so far has been demonstrated with superconducting gravity strainmeters reaching 10−10 Hz−1/2 (Moody et al.2002). Torsion-bar sensitivities have surpassed 10−7 Hz−1/2 at 0.1 Hz (Shoda et al.2014). Naturally, work on detector designs needs to be accompanied by careful selection of instrument sites, which can have a big impact on ambient seismic or infrasound fields (Berger et al.2004; Brown et al.2014), and also on the associated gravity noise.

5 CONCLUSION

In this paper we addressed for the first time the problem of modelling transient gravity perturbations produced by an earthquake during fault rupture. Since gravity changes propagate essentially instantaneously in comparison with seismic waves, gravity perturbations are generated at any distance as soon as the rupture starts. In particular, a prompt gravity perturbation is expected before the arrival of P waves, and has been computed here by an original analytical model, validated with numerical simulations. The model indicates that it would be challenging to observe prompt gravity signals within 10 s of the rupture onset with current instruments, but that they may be within the reach of high-precision gravity strainmeters currently under development.

This study sets building blocks to evaluate the detectability and information content of prompt gravity perturbations. The analysis of a potential application to earthquake early warning will be reported elsewhere, in which a few seconds of gravity signal would enable warning significantly faster than conventional systems based on seismic data. The detection of prompt gravity perturbations may also open new directions in earthquake seismology, since it consists in a direct measurement of the mass redistribution during fault rupture. How complementary is the information about the earthquake source contained in the transient gravity field and in seismic waves remains to be assessed.

Further analysis is needed to extend this study to cases where the Earth's surface affects more significantly the gravity perturbation field. Surface effects can be studied numerically, as was done here, but an analytical model of gravity perturbations in the presence of a surface would provide further insight.

We thank Eric Clévédé for discussions during the initial phase of this study and Mauricio Fuentes for assistance with verification and simplification of analytical derivations. This work was supported by NSF Grants PHY 0855313 and PHY 1205512 to UF. BFW acknowledges sabbatical support from the Université Paris Diderot and the CNRS through the APC, where part of this work was carried out. JPA acknowledges support by a grant from the Gordon and Betty Moore Foundation to Caltech. We acknowledge the financial support from the UnivEarthS Labex program at Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02) and the financial support of the Agence Nationale de la Recherche through the grant ANR-14-CE03-0014-01.

SPECFEM3D is available at http://www.geodynamics.org/cig/software/specfem3d.

REFERENCES

Accadia
T.
, et al. 
Status of the Virgo project
, 
Classical and Quantum Gravity
, 
2011
, vol. 
28
 
11
pg. 
114002
  
doi:10.1088/0264-9381/28/11/114002

Google Scholar

Crossref
Search ADS

 
Aki
K.
, 
Richards
P.G.
. , 
Quantitative Seismology
, 
2009
2nd edn
University Science Books

Google Scholar

OpenURL Placeholder Text

 
Ando
M.
, et al. 
Stable Operation of a 300-m Laser Interferometer with Sufficient Sensitivity to Detect Gravitational-Wave Events within Our Galaxy
, 
Phys. Rev. Lett.
, 
2001
, vol. 
86
 (pg. 
3950
-
3954
)

Google Scholar

Crossref
Search ADS
PubMed

 
Ando
M.
, 
Ishidoshiro
K.
, 
Yamamoto
K.
, 
Yagi
K.
, 
Kokuyama
W.
, 
Tsubono
K.
, 
Takamori
A.
. 
Torsion-bar antenna for low-frequency gravitational-wave observations
, 
Phys. Rev. Lett.
, 
2010
, vol. 
105
 
16
pg. 
161101
 

Google Scholar

Crossref
Search ADS
PubMed

 
Aso
Y.
, 
Michimura
Y.
, 
Somiya
K.
, 
Ando
M.
, 
Miyakawa
O.
, 
Sekiguchi
T.
, 
Tatsumi
D.
, 
Yamamoto
H.
. 
Interferometer design of the kagra gravitational wave detector
, 
Phys. Rev. D
, 
2013
, vol. 
88
 pg. 
043007
  
doi:
10.1103/PhysRevD.88.043007

Google Scholar

Crossref
Search ADS

 
Baker
J.G.
, 
Thorpe
J.I.
. 
Comparison of atom interferometers and light interferometers as space-based gravitational wave detectors
, 
Phys. Rev. Lett.
, 
2012
, vol. 
108
 pg. 
211101
  
doi:
10.1103/PhysRevLett.108.211101

Google Scholar

Crossref
Search ADS
PubMed

 
Beker
M.
, et al. 
Improving the sensitivity of future GW observatories in the 1–10 Hz band: Newtonian and seismic noise
, 
Gen. Relativ. Gravit.
, 
2011
, vol. 
43
 
2
(pg. 
623
-
656
)

Google Scholar

Crossref
Search ADS

 
Berger
J.
, 
Davis
P.
, 
Ekström
G.
. 
Ambient earth noise: a survey of the global seismographic network
, 
J. geophys. Res.
, 
2004
, vol. 
109
 pg. 
B11307
 

Google Scholar

Crossref
Search ADS

 
Brown
D.
, 
Ceranna
L.
, 
Prior
M.
, 
Mialle
P.
, 
Le Bras
R.
. 
The IDC seismic, hydroacoustic and infrasound global low and high noise models
, 
Pure appl. Geophys.
, 
2014
, vol. 
171
 
3–5
(pg. 
361
-
375
)

Google Scholar

Crossref
Search ADS

 
Cambiotti
G.
, 
Sabadini
R.
. 
Gravitational seismology retrieving centroid-moment-tensor solution of the 2011 tohoku earthquake
, 
J. geophys. Res.: Solid Earth
, 
2013
, vol. 
118
 
1
(pg. 
183
-
194
)

Google Scholar

Crossref
Search ADS

 
Dahlen
F.A.
, 
Tromp
J.
. , 
Theoretical Global Seismology
, 
1998
Princeton University Press

Google Scholar

OpenURL Placeholder Text

 
Dickerson
S.M.
, 
Hogan
J.M.
, 
Sugarbaker
A.
, 
Johnson
D.M.S.
, 
Kasevich
M.A.
. 
Multiaxis inertial sensing with long-time point source atom interferometry
, 
Phys. Rev. Lett.
, 
2013
, vol. 
111
 pg. 
083001
 
10.1103/PhysRevLett.111.083001

Google Scholar

Crossref
Search ADS
PubMed

 
Driggers
J.C.
, 
Harms
J.
, 
Adhikari
R.X.
. 
Subtraction of Newtonian noise using optimized sensor arrays
, 
Phys. Rev. D
, 
2012
, vol. 
86
 pg. 
102001
  
doi:10.1103/PhysRevD.86.102001

Google Scholar

Crossref
Search ADS

 
ET Science Team
. 
Einstein gravitational wave Telescope conceptual design study
, 
available from European Gravitational Observatory, document number ET-0106C-10
, 
2011

Google Scholar

OpenURL Placeholder Text

 
Fuchs
M.J.
, 
Bouman
J.
, 
Broerse
T.
, 
Visser
P.
, 
Vermeersen
B.
. 
Observing coseismic gravity change from the Japan tohoku-oki 2011 earthquake with goce gravity gradiometry
, 
J. geophys. Res.
, 
2013
, vol. 
118
 
10
(pg. 
5712
-
5721
)

Google Scholar

Crossref
Search ADS

 
Gao
Y.
, 
Chen
X.
, 
Hu
H.
, 
Zhang
J.
. 
Early electromagnetic waves from earthquake rupturing: I. theoretical formulations
, 
Geophys. J. Int.
, 
2013
, vol. 
192
 
3
(pg. 
1288
-
1307
)

Google Scholar

Crossref
Search ADS

 
Gao
Y.
, 
Chen
X.
, 
Hu
H.
, 
Wen
J.
, 
Tang
J.
, 
Fang
G.
. 
Induced electromagnetic field by seismic waves in earth's magnetic field
, 
J. geophys. Res.
, 
2014
, vol. 
119
 
7
(pg. 
5651
-
5685
)

Google Scholar

Crossref
Search ADS

 
Harms
J.
, 
DeSalvo
R.
, 
Dorsher
S.
, 
Mandic
V.
. 
Simulation of underground gravity gradients from stochastic seismic fields
, 
Phys. Rev. D
, 
2009
, vol. 
80
 pg. 
122001
  
doi:
10.1103/PhysRevD.80.122001

Google Scholar

Crossref
Search ADS

 
Harms
J.
, 
Slagmolen
B.J.J.
, 
Adhikari
R.X.
, 
Miller
M.C.
, 
Evans
M.
, 
Chen
Y.
, 
Müller
H.
, 
Ando
M.
. 
Low-frequency terrestrial gravitational-wave detectors
, 
Phys. Rev. D
, 
2013
, vol. 
88
 pg. 
122003
  
doi:10.1103/PhysRevD.88.122003

Google Scholar

Crossref
Search ADS

 
Hohensee
M.
, 
Lan
S.
, 
Houtz
R.
, 
Chan
C.
, 
Estey
B.
, 
Kim
G.
, 
Kuan
P.
, 
Müller
H.
. 
Sources and technology for an atomic gravitational wave interferometric sensor
, 
Gen. Relati. Gravit.
, 
2011
, vol. 
43
 
7
(pg. 
1905
-
1930
)

Google Scholar

Crossref
Search ADS

 
Houston
H.
. 
Influence of depth, focal mechanism, and tectonic setting on the shape and duration of earthquake source time functions
, 
J. geophys. Res.: Solid Earth
, 
2001
, vol. 
106
 
B6
(pg. 
11137
-
11150
)

Google Scholar

Crossref
Search ADS

 
Imanishi
Y.
, 
Sato
T.
, 
Higashi
T.
, 
Sun
W.
, 
Okubo
S.
. 
A network of superconducting gravimeters detects submicrogal coseismic gravity changes
, 
Science
, 
2004
, vol. 
306
 
5695
(pg. 
476
-
478
)

Google Scholar

Crossref
Search ADS
PubMed

 
Jekeli
C.
. 
Potential theory and static gravity field of the earth, in
, 
Treatise on Geophysics
, 
2007
Elsevier
(pg. 
11
-
42
) 
Vol. 3

Google Scholar

OpenURL Placeholder Text

 
John
J.
, 
Draper
N.
. 
An alternative family of transformations
, 
Appl. Stat.
, 
1980
(pg. 
190
-
197
)

Google Scholar

OpenURL Placeholder Text

 
Komatitsch
D.
, 
Tromp
J.
. 
Introduction to the spectral element method for three-dimensional seismic wave propagation
, 
Geophys. J. Int.
, 
1999
, vol. 
139
 
3
(pg. 
806
-
822
)

Google Scholar

Crossref
Search ADS

 
Komatitsch
D.
, 
Vilotte
J.-P.
. 
The spectral element method: an efficient tool to simulate the seismic response of 2d and 3d geological structures
, 
Bull. seism. Soc. Am.
, 
1998
, vol. 
88
 
2
(pg. 
368
-
392
)

Google Scholar

OpenURL Placeholder Text

 
LIGO Scientific Collaboration
. 
LIGO: the Laser Interferometer Gravitational-Wave Observatory
, 
Rep. Prog. Phys.
, 
2009
, vol. 
72
 pg. 
076901
  
doi:10.1088/0034-4885/72/7/076901
Crossref
Search ADS

 
Lück
H.
, et al. 
The upgrade of GEO600
, 
J. Phys.: Conf. Series
, 
2010
, vol. 
228
 pg. 
012012
  
doi:10.1088/1742-6596/228/1/012012

Google Scholar

Crossref
Search ADS

 
Matsuo
K.
, 
Heki
K.
. 
Coseismic gravity changes of the 2011 Tohoku-Oki earthquake from satellite gravimetry
, 
Geophys. Res. Lett.
, 
2011
, vol. 
38
 pg. 
L00G12
  
doi:10.1029/2011GL049018

Google Scholar

Crossref
Search ADS

 
Moody
M.V.
, 
Paik
H.J.
, 
Canavan
E.R.
. 
Three-axis superconducting gravity gradiometer for sensitive gravity experiments
, 
Rev. Sci. Instrum.
, 
2002
, vol. 
73
 
11
(pg. 
3957
-
3974
)

Google Scholar

Crossref
Search ADS

 
Neumeyer
J.
. 
Xu
G.
. 
Superconducting gravimetry, in
, 
Sciences of Geodesy – I
, 
2010
Springer
(pg. 
339
-
413
)

Google Scholar

OpenURL Placeholder Text

 
Okubo
S.
. 
Potential and gravity changes raised by point dislocations
, 
Geophys. J. Int.
, 
1991
, vol. 
105
 
3
(pg. 
573
-
586
)

Google Scholar

Crossref
Search ADS

 
Okubo
S.
. 
Gravity and potential changes due to shear and tensile faults in a half-space
, 
J. geophys. Res.
, 
1992
, vol. 
97
 
B5
(pg. 
7137
-
7144
)

Google Scholar

Crossref
Search ADS

 
Shoda
A.
, 
Ando
M.
, 
Ishidoshiro
K.
, 
Okada
K.
, 
Kokuyama
W.
, 
Aso
Y.
, 
Tsubono
K.
. 
Search for a stochastic gravitational-wave background using a pair of torsion-bar antennas
, 
Phys. Rev. D
, 
2014
, vol. 
89
 pg. 
027101
 
10.1103/PhysRevD.89.027101

Google Scholar

Crossref
Search ADS

 
Sun
W.
, 
Okubo
S.
, 
Fu
G.
, 
Araya
A.
. 
General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric earth modelépplicable to deformed earth surface and space-fixed point
, 
Geophys. J. Int.
, 
2009
, vol. 
177
 
3
(pg. 
817
-
833
)

Google Scholar

Crossref
Search ADS

 
Takeuchi
H.
, 
Saito
M.
. 
Seismic surface waves
, 
Methods in computational physics
, 
1972
, vol. 
11
 (pg. 
217
-
295
)

Google Scholar

OpenURL Placeholder Text

 
Wang
L.
, 
Shum
C.
, 
Jekeli
C.
. 
Gravitational gradient changes following the 2004 December 26 Sumatra–Andaman Earthquake inferred from GRACE
, 
Geophys. J. Int.
, 
2012a
, vol. 
191
 
3
(pg. 
1109
-
1118
)

Google Scholar

Crossref
Search ADS

 
Wang
L.
, et al. 
Coseismic slip of the 2010 Mw 8.8 Great Maule, Chile, earthquake quantified by the inversion of GRACE observations
, 
Earth planet. Sci. Lett.
, 
2012b
, vol. 
335
 (pg. 
167
-
179
)

Google Scholar

Crossref
Search ADS

 

APPENDIX A: CALCULATING GRAVITY PERTURBATIONS USING SPHERICAL HARMONICS

A straightforward and possibly more intuitive, but slightly more involved method to calculate gravity perturbations is to directly integrate over the field of density perturbations produced by a double-couple source according to
\begin{eqnarray} \delta \psi (\boldsymbol{r}_0\,,t)=-G\int {\rm d} V\,\frac{\delta \rho (\boldsymbol{r}\,,t)}{|\boldsymbol{r}-\boldsymbol{r}_0|}. \end{eqnarray}
(A1)
The integrand can be expanded into its spherical multipoles. The integration over the radial coordinate r is divided into two intervals: 0 < r < r0 and r0 < r. Over the first interval, one obtains the exterior spherical multipole expansion:
\begin{eqnarray} \delta \psi _{\rm ext}(\boldsymbol{r}_0\,,t) = G \sum \limits _{l=0}^\infty \sum \limits _{m=-l}^l I_l^m(\boldsymbol{r}_0)^* \cdot \int \limits _0^{r_0}{\rm d} r\,r^2\int {\rm d}\Omega \,\delta \rho (\boldsymbol{r},t)R_l^m(\boldsymbol{r}),\nonumber \\ \end{eqnarray}
(A2)
where
\begin{eqnarray} R_l^m(\boldsymbol{r}) &\equiv &\sqrt{\frac{4\pi }{2l+1}}r^lY_l^m(\theta ,\phi )\nonumber\\ I_l^m(\boldsymbol{r}) &\equiv &\sqrt{\frac{4\pi }{2l+1}}\frac{1}{r^{l+1}}Y_l^m(\theta ,\phi ) \end{eqnarray}
(A3)
are the regular and irregular solid spherical harmonics (in Racah's normalization), respectively, |$Y_l^m(\cdot )$| the spherical harmonics, and dΩ = dϕ dθsin (θ). The corresponding expression for the interior spherical multipole expansion is
\begin{eqnarray} \delta \psi _{\rm int}(\boldsymbol{r}_0\,,t) = G \sum \limits _{l=0}^\infty \sum \limits _{m=-l}^l R_l^m(\boldsymbol{r}_0)^* \cdot \int \limits _{r_0}^\infty {\rm d} r\,r^2\int {\rm d}\Omega \,\delta \rho (\boldsymbol{r},t)I_l^m(\boldsymbol{r}).\nonumber \\ \end{eqnarray}
(A4)
Inserting the density perturbation of eq. (3) into the exterior multipole expansion of the gravity potential we have
\begin{eqnarray} \delta \psi _{\rm ext}(\boldsymbol{r}_0\,,t) &=& G \sum \limits _{l=0}^\infty \sum \limits _{m=-l}^l I_l^m(\boldsymbol{r}_0)^* \cdot \int \limits _0^{r_0}{\rm d} r\,r^2\Delta (r,t)\nonumber\\ &&\cdot \int {\rm d}\Omega \,R_{\rm P}(\theta ,\phi )R_l^m(\boldsymbol{r}). \end{eqnarray}
(A5)
The integral over angles can be carried out by expressing the radiation pattern of the density field in eq. (4) in terms of the spherical harmonics |$Y_2^1$| and |$Y_2^{-1}$|⁠,
\begin{eqnarray} R_{\rm P}(\theta ,\phi ) =2\sqrt{2\pi /15}\,\left(Y_2^{-1}(\theta ,\phi )^*-Y_2^1(\theta ,\phi )^*\right), \end{eqnarray}
(A6)
and making use of the orthogonality relation
\begin{eqnarray} \int {\rm d}\Omega \, Y_l^m(\theta ,\phi )Y_{l^{\prime }}^{m^{\prime }}(\theta ,\phi )^*=\delta _{ll^{\prime }}\delta _{mm^{\prime }}. \end{eqnarray}
(A7)
This leads to
\begin{eqnarray} \delta \psi _{\rm ext}(\boldsymbol{r}_0\,,t) &=& G \frac{4\pi }{5}\frac{1}{r_0^3} \int \limits _0^{r_0}{\rm d} r\,r^4\Delta (r,t)\nonumber\\ &&\times \sum \limits _{m=-1, 1} Y_2^m(\theta _0,\phi _0)^*\int {\rm d}\Omega \,R_{\rm P}(\theta ,\phi )Y_2^m(\theta ,\phi ) \end{eqnarray}
(A8)
Further simplification shows that the angular dependence is given by the quadrupole radiation pattern RP(θ0, ϕ0). The integral over the radius can be simplified considerably by integration by parts. An expression for the interior multipole expansion is obtained by a similar procedure. The solution |$\delta \psi (\boldsymbol{r}_0\,,t)=\delta \psi _{\rm ext}(\boldsymbol{r}_0\,,t)+\delta \psi _{\rm int}(\boldsymbol{r}_0\,,t)$| for the gravity potential perturbation can then be written in the form given in eq. (10).
The form of the early gravity perturbation, eq. (12), suggests that one can obtain this result from a simple effective source term. Due to the quadrupolar form of the radiation pattern (i.e. it involves only spherical harmonics of degree 2), we can represent the source by a mass quadrupole moment
\begin{eqnarray} Q_{ij} = \int {\rm d} V\, \delta \rho (3x_i x_j - \delta _{ij} r^2) \end{eqnarray}
(A9)
and zero monopole and dipole moments. Such a quadrupolar density distribution generates the following exterior gravity potential:
\begin{eqnarray} \delta \psi (\boldsymbol{r}_0, t) = -\frac{G}{r_0^3} \sum _{i,j} Q_{ij}(t) (\boldsymbol{e}_i\cdot \boldsymbol{e}_{r_0})(\boldsymbol{e}_j\cdot \boldsymbol{e}_{r_0}). \end{eqnarray}
(A10)
The integral in eq. (A9) can be solved again by expanding the integrand into its multipoles. For early times, t < r0/α, the same result is obtained for the gravity perturbation with the only non-zero components of the quadrupole moment tensor
\begin{eqnarray} Q_{xz}(t) = Q_{zx}(t) = 3 I_2[M_0](t). \end{eqnarray}
(A11)
Thereby, we have established an effective source model for prompt gravity perturbations generated by a double-couple.

APPENDIX B: SOURCE MODEL OF NUMERICAL SIMULATION

We consider a circular pulse-like rupture of finite duration with cosine slip rate function and constant rupture speed:
\begin{eqnarray} \dot{s}(r,t)&=&\frac{2\delta }{T}\sin \left(\frac{\pi }{T}(t-r/v_{\rm rup})\right)^2\nonumber\\ &&\times \Theta (t-r/v_{\rm rup})\Theta (T-t+r/v_{\rm rup})\Theta (v_{\rm rup}\tau -r) \end{eqnarray}
(B1)
where Θ( · ) denotes the unit step function. In words, the fault slip δ at distance r from the hypocentre builds up over a rise timeT. The rupture propagates radially outwards with velocity vrup, until it reaches the distance vrupτ. Therefore, τ can be regarded as the duration of the rupture, but the final fault slip occurs at time τ + T.
The moment function for a circular fault rupture can be calculated as
\begin{eqnarray} M_0(t)=2\pi \mu \int \limits _0^t{\rm d} t^{\prime }\int \limits _0^\infty {\rm d} r\,r\dot{s}(r,t^{\prime }), \end{eqnarray}
(B2)
where μ is the shear modulus. Using the slip velocity model of eq. (B1), the moment function is found to be
\begin{eqnarray} &&\!\!\!\!&&{M_0(t)=\frac{\mu \,\delta \, v_{\rm rup}^{2}T^{2}}{12\pi^{2}}\cdot} \\ &&\!\!\!\!\left\lbrace {\begin{array}{c@{\quad}c}-6\pi u+4\pi^{3}u^{3}+3\sin (2\pi u), & t\le T\\ 2\pi (-3+\pi^{2}(2+6(u-1)u)), & T<t\le \tau \\ -2\pi \big [3-3u+2\pi^{2}((u-1)^{3}-3uv^{2}+2v^{3})&\\ +\, 3v\cos (2\pi (u-v))\big ]-3\sin (2\pi (u-v))& \tau <t\le \tau +T\\ 12\pi^{3}v^{2}, & \tau +T < t\end{array}} \right.\nonumber \\ \end{eqnarray}
(B3)
with u ≡ t/T, and v ≡ τ/T. After the rupture ends at t = τ + T, the moment function stays at a constant value of μ δ π(vrupτ)2, and according to eq. (18) the gravity acceleration grows as ∼t2 until P waves reach |$\boldsymbol{r}_0$|⁠.
© The Authors 2015. Published by Oxford University Press on behalf of The Royal Astronomical Society.
Subject
Gravity, Geodesy and Tides
Issue Section:
Gravity, geodesy and tides
Download all slides