Introduction

Evapotranspiration (ET) is one of the major elements of the hydrologic cycle, and its accurate predictions is of paramount importance for many investigations such as irrigation system design and management, hydrologic water balance, crop yield simulation, irrigation scheduling, drainage studies, agricultural and forest meteorology, and water resources planning and management (Banihabib et al. 2012; Kumar et al. 2002; Valipour 2014c, d, e, f, g, h).

The most important parameters that affect on variations of evapotranspiration are air temperature, humidity, wind speed, and sun radiation (Pejic et al. 2015; Valipour 2014a, i, j, k; Wrachien and Mambretti 2015; Yannopoulos et al. 2015). At first, there is a distinction between reference and actual evapotranspiration. Reference evapotranspiration corresponds to the amount of water that would return to the atmosphere in case of moisture redundancy, for a reference crop [e.g., alfalfa (ETr) or grass (ET0)], from a standard surface and to then apply an appropriate empirical crop coefficient, which accounts for the difference between the standard surface and crop ET (Tzimopoulos et al. 2007; Valipour 2015a, b, c; Valipour et al. 2012).

ET0 refers to the water emitted from a unit ground area covered with a reference plant, unstressed and healthy as well as with ample water supply (Walter et al. 2002). The ET0 is used to quantify evapotranspirative demand within a zone and to forecast crop evapotranspiration when the ET0 is multiplied by a crop coefficient (K c) to determine for differences between the grass and plant evapotranspiration (Allen et al. 1998; Schuch and Burger 1997).

Measurements of pan evaporation are spatiotemporally limited, especially in developing countries. In locations where pan evaporation measurements are sparse, theoretical forecasts can be used to estimate it from other existing data, which depend strongly on the local conditions. Evapotranspiration is a function of wind speed, temperature, and humidity. Solar radiation is also a significant parameter for evapotranspiration. All of these factors do not act independently. Wind varies the humidity, and if the humidity is low, the evapotranspiration rate is higher. At the same time, air temperature affects surface temperature and humidity. These parameters all contribute to evaporation with temperature likely being the dominant factor influencing evapotranspiration (Rahimikhoob 2009).

Where pan evaporation data are not available, evapotranspiration can be characterized by evapotranspiration models using weather variables. Among them, the Penman model is most frequently used for evapotranspiration prediction. The Penman model requires five climatic parameters: temperature, relative humidity, wind, saturation vapor pressure, and net radiation. It also uses complicated unit conversions and lengthy computations (Wu 1997).

Many researchers have evaluated the reliability of the Penman–Monteith (PM) model for predicting ET0 (McNaughton and Jarvis 1984; Allen 1986; Allen et al. 1989; De Souza and Yoder 1994; Chiew et al. 1995). Jensen et al. (1990) analyzed the performance of 20 different models against lysimeter measured ET for 11 stations located in various climatic regions around the world. The PM model ranked as the best method for all climatic situations. However, the ranking of other models varied, depending on their local calibration and conditions.

Abtew and Obeysekera (1995) and Abtew (1996) found that the Penman–Monteith model was well suited to predict evapotranspiration from cattails (Typha domingensis), mixed marsh vegetation, and an open water/algae system; however, that calibrated simpler radiation-based methods also provided reasonable forecasts.

Potential evapotranspiration (PET), rather than actual evapotranspiration (AET), is a common input for empirical methods because it offers an upper limit to evapotranspirative water losses. PET is a function of vapor pressure gradient, available energy, and vegetation type (Douglas et al. 2009). In predicting PET, a clear definition of the “best” method for calculation is not evident and the model choice is often subjective. Verstraeten et al. (2008) presented a comprehensive review of the scientific articles on models for evaluating PET and mentioned that the selection of one model from the many is primarily dependent on the goals of the investigation and the type of available data. For example, Weib and Menzel (2008) compared the Priestley–Taylor (PT) method, two methods based on the Penman–Monteith (PM) equation and the Hargreaves method, a temperature-based method for predicting PET in a global-scale hydrologic method.

However, more study is needed on irrigation management to establish the appropriate model to be applied for evaluating crop evapotranspiration (ET), to avoid the excess or deficit water application, waterlogging, and soil salinity (Eslamian et al. 2009). Operational software tools in the domains specified above require the evaluation of ET0 and the procedures to do that have been repeatedly implemented in software applications. This is one of the reasons that why there is an increasing demand for modular methods in model development (Jones et al. 2001). Reference evapotranspiration can be measured by lysimeters; however, this approach is very expensive and not easy to use (Valipour 2014l, m, 2015e). Many authors have attempted to estimate the evaporation through the indirect models using the weather parameters; however, some of these methods require the data, which cannot easily be measured (Rosenberry et al. 2007).

Today, applications of modeling and regression methods have been widely spread in different fields of the science. These methods were applied for increasing the quality of forecasts using the sample data sets from experiments and different investigations. Appropriate use of these methods is very useful for resolve of uncertainties and results of predictions, when obtain of information is difficult and sometimes impossible.

The most frequently used statistical methods are known as frequentist (or classical) methods. These methods assume that unknown parameters are the fixed constants, and they define probability using limiting relative frequencies. Bayesian methods offer an alternative approach; they treat the parameters as random variables and define probability as “degrees of belief” (i.e., the probability of an event is the degree to believe the event is true). The term “Bayesian” comes from the prevalent usage of Bayes’ theorem, which was named after the Reverend Thomas Bayes, an eighteenth-century Presbyterian minister (Rathnayake 2010).

Bayesian analysis is a mode of inductive reasoning that has been applied in a lot of scientific disciplines. A distinctive feature of the Bayesian approach is that it permits the researcher to use sample (data) and prior (expert judgment) information in a logically consistent manner in making inferences. This is done by using Bayes’ theorem to produce a “post-data” or posterior distribution for the model variables. Using Bayes’ theorem, prior (or initial) values are transformed to post-data views. This transformation can be viewed as a learning process. The posterior distribution is calculated by the variances of the prior and sample information. If the variance of the prior information is smaller than the variance of the sampling information, then a higher weight is assigned to the prior information. On the other hand, if the variance of the sample information is smaller than the variance of the prior information, then a higher weight is assigned to the sample information causing the posterior forecast to be closer to the sample information (Chulani et al. 1998; Singh 2014).

Since their introduction by Royston and Altman (1994), the regression methods based on fractional polynomial (FP) transformation of continuous predictor(s) have found gradual acceptance as a useful technique of analysis which retains such predictors as continuous in the model. The robust regression using functions related to the least squares has been the subject of intense research (Royston and Sauerbrei 2007). Demoster et al. (1980) discussed statistical properties of the predictions under the assumption that the observation errors are independent normal. Coleman et al. (1980) developed a high-quality set of routines to calculate robust predictions for eight weight functions.

The superiority of regression models to artificial intelligence techniques such as ANFIS, ANN, and SVM is that regression models have the less complexity. In addition, these models give us the formula or relationship and have an acceptable accuracy. Although application of nonlinear regression and Bayesian approach has been surveyed in the various fields of hydrology and water management such as irrigation canal demands (Ticlavilca et al. 2013), low flow indices (Joshi et al. 2013), land surface temperature (Ghosh and Joshi 2014), catchment modeling (Marshall et al. 2007), nutrient loading (Vigiak and Bende-Mich 2013; Wellen et al. 2012), heat flux (Ershadi et al. 2013; Yao et al. 2014), solar radiation (Iizumi et al. 2012), and streamflow modeling (Block and Rajagopalan 2009; Liang et al. 2013), there are few studies about application of them in estimation of ET (Bachour et al. 2014; Izadifar and Elshorbagy 2010; Tabari et al. 2012; Zhu et al. 2013). However, these studies focus on some limited methods and/or use low recorded data. Furthermore, comparison of the nonlinear regression methods and Bayesian approach has not been investigated in arid regions (Valipour 2013a, b). In the present paper, the attempts are made to apply MFP, Bayesian regression, and robust regression models to estimate reference evapotranspiration values, in three arid regions of Iran in which water crises are considerable (Mahdizadeh Khasraghi et al. 2015; Valipour et al. 2015), using temperature data.

Materials and methods

Fractional polynomials

Simple power transformations of a covariate have long been used informally in data analysis in cases when nonlinearity was suspected. General power models were proposed by Box and Tidwell (1962). Royston and Altman (1994) formalized the simple power models and called them fractional polynomials of degree 1 (FP1), and extended them to FPs of higher degree. Ignoring the intercept term (β 0), a polynomial of degree m in a single covariate X may be written:

$$\beta_{1} X^{1} + \, \beta_{2} X^{2} + \cdots + \beta_{\text{m}} X^{\text{m}}$$
(1)

In the generalization to an FP function of degree m, written FP m(X), the indices 1,…, m are replaced with the powers p 1, …, p m , giving:

$${\text{FP}}\,m\left( X \right) = \beta_{1} X^{{{\text{P}}1}} + \beta_{2} X^{{{\text{P}}2}} + \cdots + \beta_{\text{m}} X^{\text{Pm}}$$
(2)

As proposed by Royston and Altman (1994), the powers p 1, …, p m are chosen from a restricted set, S = {−2, −1, −0.5, 0, 0.5, 1, 2, 3}, where X 0 denotes logX. No subsequent changes to S have been adopted. The set includes no transformation (p = 1) and the reciprocal, logarithmic, square root, and square transformations. FP2 functions take the form:

$${\text{FP}}2 = \beta_{1} X^{{{\text{P}}1}} + \beta_{2} X^{{{\text{P}}2}}$$
(3)

Or

$${\text{FP}}2 = \beta_{1} X^{{{\text{P}}1}} + \beta_{2} X^{{{\text{P}}1}} \log X$$
(4)

The latter being the so-called repeated-powers function obtained in the mathematical limit p 2 → p 1 (Royston and Sauerbrei 2005).

Consider a linear regression model:

$$Y = X\beta_{2} + e$$
(5)

where Y is an n-vector of observed responses, X is an n × k matrix representing k covariates, β is a k-vector of parameters and e is an n-vector of residuals with E(e) = 0, var(e) = σ 2 I. The ordinary least squares (OLS) estimator of β is \(\hat{\beta } = (X^{{\prime }} X)^{ - 1} X^{{\prime }} Y\), and the vector of fitted values is \(\hat{Y} = X\hat{\beta } = HY\). The matrix \(H = X(X^{{\prime }} X)^{ - 1} X^{{\prime }}\) is usually called the “hat” matrix. Its diagonal elements \(h_{i} = H_{ij} x_{i} (X^{{\prime }} X)^{ - 1} x_{i}^{{\prime }}\) are termed leverages. In the special case of a single covariate, x, the leverages are as follows given (Belsley et al. 1980; Royston and Sauerbrei 2007):

$$h_{i} = \frac{1}{n} + \frac{{(x_{i} - \bar{x})^{2} }}{{\sum\nolimits_{j = 1}^{n} {(x_{j} - \bar{x})^{2} } }}$$
(6)

The leverage is then a linear function of the squared distance of xi from the covariate mean, \(\bar{x}\).

Multivariable fractional polynomial modeling

The central problem of modeling is the joint effect of several covariates, at least two of which are continuous and some may be categorical or binary. At the same time, the model must be simplified, both/either dropping nonsignificant variables and/or by reducing the complexity of FP functions fitted to continuous covariates. A solution to finding a model in this situation was proposed by Royston and Altman (1994) and further refined by Sauerbrei and Royston (1999). In essence, it is impractical to try all combinations of powers for finding the best-fitting set of FP functions for all of the candidate continuous variables, and an iterative algorithm is needed. This was termed the MFP procedure by Sauerbrei and Royston (1999). It combines backward elimination of variables with a search for the best FP functions of continuous covariates. First, a significance level such as 0.05 is chosen. Next, the fitting order is determined by fitting a model linear in all variables and eliminating each variable singly, which is the first step of a conventional backward elimination procedure. The p values from the tests are used to order the variables, from the most to the least significant. Having imposed an order, each X is considered in turn. If an X is categorical or binary, a standard likelihood ratio test is performed to determine whether it should be dropped or not. If an X is continuous, the FP model selection procedure is applied to determine the best FP (or to eliminate X). The procedure cycles through the variables in the same order until the selected variables and FP functions do not change. Typically, two or three cycles are required for convergence (Royston and Sauerbrei 2005).

Robust regression

The models described in linear regression models are based on certain assumptions, such as a normal distribution of errors in the observed responses. If the distribution of errors is asymmetric or prone to outliers, model assumptions are invalidated, and parameter estimates, confidence intervals, and other computed statistics become unreliable. The Statistics Toolbox function robust fit is useful in these cases. The function implements a robust fitting method that is less sensitive than OLS to large changes in small parts of the data (Matlab Statistics Toolbox 2010).

Robust regression works by assigning a weight to each data point. Weighting is done automatically and iteratively using a process called iteratively reweighted least squares. In the first iteration, each point is assigned equal weight and model coefficients are estimated using ordinary least squares. At subsequent iterations, the weights are recomputed so that the points farther from model predictions in the previous iteration are given a lower weight. The model coefficients are then recomputed using weighted least squares (WLS). The process continues until the values of the coefficient estimates converge within a specified tolerance (Matlab Statistics Toolbox 2010).

Robust demo demonstrates the difference between ordinary (least squares) regression and robust regression. It displays a scatter plot of X and Y values, where Y is roughly a linear unction of X, but one point is an outlier (it falls far from the line). The bottom of the figure shows the fitted equations using least squares and robust fitting, plus an estimate of the root mean squared error from both. Leverage is a measure of how much influence that point has on the least squares fit. Weight is the weight that point was given in the robust fit. Robust demo (X, Y) uses X and Y data that supply, in place of the sample data supplied with the function (Matlab Statistics Toolbox 2010).

Bayesian regression

Bayesian regression, the theory specialized adaptation is including the development of multivariate regression models, which clearly consider two sources of previous and experimental information.

Bayesian regression analysis is including development of model or prediction of the relations among variables. For example, a prediction equation can be the following linear form (Eq. 7).

$$y = b_{0} + b_{1} x_{1} + b_{2} x_{2} + \cdots + b_{\text{p}} x_{\text{p}}$$
(7)

where Y is the dependent variable, independent variables are predicted by X i , and the aim is numerical determine of b j coefficients.

The Bayesian model makes possible the decision in short time with development of data and judgments and continue of modeling.

Suppose that we are interested in estimating θ from data y = {y 1, …, y n } using a statistical model described by a density p(y|θ). Bayesian philosophy states that θ cannot be determined exactly, and uncertainty about the parameter is expressed through probability statements and distributions. Also, we can say that θ follows a normal distribution with mean 0 and variance 1, if it is believed that this distribution best describes the uncertainty associated with the parameter. The following steps describe the essential elements of Bayesian inference:

  1. 1.

    A probability distribution for θ is formulated as π(θ), which is known as the prior distribution, or just the prior. The prior distribution expresses beliefs (e.g., on the mean, the spread, and the skewness) about the parameter before examining the data.

  2. 2.

    Given the observed data y, choose a statistical model p(y|θ) to describe the distribution of y given θ.

  3. 3.

    Update of beliefs about θ by combining information from the prior distribution and the data through the calculation of the posterior distribution, p(y|θ).

The third step is carried out using Bayes’ theorem, which enables to combine the prior distribution and the model in the following way:

$$p(y\left| {\theta )} \right. = \frac{p(\theta .y)}{p(y)} = \frac{{p(y\left| {\theta )\pi (\theta )} \right.}}{p(y)} = \frac{{p(y\left| {\theta )\pi (\theta )} \right.}}{{\int {p(y\left| {\theta )\pi (\theta )} \right.{\text{d}}\theta } }}$$
(8)

The quantity

$$p(y) = \int {p(y\left| {\theta )\pi (\theta )} \right.{\text{d}}\theta }$$
(9)

is the normalizing constant of the posterior distribution. This quantity p(y) is also the marginal distribution of y, and it is sometimes called the marginal distribution of the data. The likelihood function of θ is any function proportional to p(y|θ); that is L(θ) ∝ p(y|θ).

In this study, daily grass reference ET (ET0) is determined using the FAO Penman–Monteith (FAO-PM) approach (Allen et al. 1998). There are many studies that applied FAO-PM model as a base model for calculation of reference ET in different regions of Iran (Rahimi et al. 2014; Valipour 2012c, d, e, f, 2015d; Valipour and Eslamian 2014). The FAO-PM equation for a grass reference crop is defined as:

$${\text{ET}}_{0} = \frac{{0.408\varDelta (R_{n} - G) + \gamma (900/(T + 273))u_{2} (e_{s} - e_{a} )}}{{\varDelta + \gamma (1 + 0.34u_{2} )}}$$
(10)

where ET0 is the evapotranspiration (mm day−1), R n is the net radiation (MJ m2 day−1), G is the soil heat flux (MJ m2 day−1), T is the mean daily air temperature (°C), u 2 is the mean daily wind speed at 2 m height (m s−1), e s  − e a is the saturation vapor pressure deficit (kPa °C−1), and γ is the psychometric constant (kPa °C−1).

In this study, three models were performed including MFP, Bayesian regression, and robust regression models. All of the models were designed with three parameters as input data, including solar radiation (Ra), mean temperature (T mean), and T max − T min.

Study area

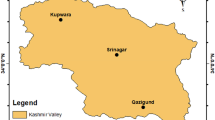
In this study, three synoptic stations have been used that have at least 14-year data to avoid the errors due to the problem of short record length. These stations are located on central part of Iran with an arid environment. Figure 1 and Table 1 show the position and geographic characteristics of Esfahan, Kashan, and Ardestan stations, respectively. All of the information is in monthly scale and has been collected from Islamic Republic of Iran Meteorological Organization (IRIMO) at this link: http://irimo.ir/eng/index.php.

Fig. 1
figure 1

Position of Esfahan, Kashan, and Ardestan in Iran

Full size image
Table 1 Geographic characteristics of the stations
Full size table

To evaluate the performance of these models in monthly ET0 estimates, between the calculated and predicted ET, the root mean square error (RMSE) is applied as given:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(\left( {\frac{{Y_{\text{obs}} - Y_{\text{calc}} }}{{Y_{\text{obs}} }}} \right)^{2} } }$$
(11)

where Y calc is the calculated value and Y est is estimation of the models.

Results and discussions

Multivariable fractional polynomial modeling

The results of statistical parameters of MFP model are given in Table 2. In addition, Figs. 2, 3 and 4 show the predicted values of ET versus the calculated values of ET.

Table 2 Statistical parameters of the MFP model for ET prediction
Full size table
Fig. 2
figure 2

Comparison of the ET predicted with MFP model versus the calculated values by FAO-PM for Esfahan station

Full size image
Fig. 3
figure 3

Comparison of the ET predicted with MFP model versus the calculated values by FAO-PM for Kashan station

Full size image
Fig. 4
figure 4

Comparison of the ET predicted with MFP model versus the calculated values by FAO-PM for Ardestan station

Full size image

To evaluate the MFP model, the amount of ET estimated by this model was plotted versus the calculated values. These results are shown for Esfahan, Kashan, and Ardestan stations in Figs. 2, 3 and 4, respectively. The best performance of the MFP model was obtained for Kashan than Esfahan and Ardestan stations.

Considering the obtained results, in this study, it could be stated that use of MFP model can predict (R 2 > 0.95) the amount of ET in different stations, and this application can be added to the other applications of MFP model.

The formula obtained from MFP model for Esfahan, Kashan, and Ardestan stations are shown in Eqs. 12, 13, and 14, respectively.

$${\text{ET}} = - 323.91 + 54.6\left( {\frac{\text{Ra}}{1000}} \right)^{ - 1} + 293.42\left( {\frac{\text{Ra}}{1000}} \right)^{0.5} + 23.71\left( {\frac{{T_{\text{mean}} + 3.4}}{10}} \right) + 11.74\left( {\frac{{T{}_{\hbox{max} } - T{}_{\hbox{min} }}}{10}} \right)^{3} - 16.62\left( {\frac{{T{}_{\hbox{max} } - T{}_{\hbox{min} }}}{10}} \right)^{3} {\text{Ln}}\left( {\frac{{T{}_{\hbox{max} } - T{}_{\hbox{min} }}}{10}} \right)$$
(12)
$${\text{ET}} = - 13.304 + 63.466\left( {\frac{\text{Ra}}{1000}} \right)^{2} + 4.172\left( {\frac{{T_{\text{mean}} }}{10}} \right)^{2} + 14.324\left( {\frac{{T{}_{\hbox{max} } - T{}_{\hbox{min} }}}{10}} \right)$$
(13)
$${\text{ET}} = - 39.147 + 62.267\left( {\frac{\text{Ra}}{1000}} \right)^{2} + 9.524\left( {\frac{{T_{\text{mean}} }}{10}} \right)^{2} + 56.422\left( {\frac{{T{}_{\hbox{max} } - T{}_{\hbox{min} }}}{10}} \right)$$
(14)

Robust regression

The results of statistical parameters of robust regression model are given in Table 3. In addition, Figs. 5, 6 and 7 show the predicted values of ET versus the calculated values of ET.

Table 3 Statistical parameters of the robust regression model for ET prediction
Full size table
Fig. 5
figure 5

Comparison of the ET predicted with robust regression model versus the calculated values by FAO-PM for Esfahan station

Full size image
Fig. 6
figure 6

Comparison of the ET predicted with robust regression model versus the calculated values by FAO-PM for Kashan station

Full size image
Fig. 7
figure 7

Comparison of the ET predicted with robust regression model versus the calculated values by FAO-PM for Ardestan station

Full size image

To evaluate the robust regression model, the amount of ET estimated by this model was plotted versus the calculated values. These results are shown for Esfahan, Kashan, and Ardestan stations in Figs. 5, 6 and 7, respectively. The maximum value of the correlation coefficient was obtained for Ardestan; however, the minimum value of RMSE belongs to Kashan.

The formula obtained from robust regression model for Esfahan, Kashan, and Ardestan stations are shown in Eqs. 15, 16, and 17, respectively.

$$ET = - 19.6047 + 2.8297T_{\text{mean}} - 0.7866(T_{\hbox{max} } - T_{\hbox{min} } ) + 0.0753{\text{Ra}}$$
(15)
$${\text{ET}} = - 51.9819 + 2.022T_{\text{mean}} - 0.0465(T_{\hbox{max} } - T_{\hbox{min} } ) + 0.1061{\text{Ra}}$$
(16)
$${\text{ET}} = - 87.4207 + 3.9657T_{\text{mean}} + 2.381(T_{\hbox{max} } - T_{\hbox{min} } ) + 0.1195{\text{Ra}}$$
(17)

Bayesian regression

The results of statistical parameters of Bayesian regression model are given in Table 4. In addition, Figs. 8, 9, and 10 show the predicted values of ET versus the calculated values of ET.

Table 4 Statistical parameters of the Bayesian regression model for ET prediction
Full size table
Fig. 8
figure 8

Comparison of the ET predicted with Bayesian regression model versus the calculated values by FAO-PM for Esfahan station

Full size image
Fig. 9
figure 9

Comparison of the ET predicted with Bayesian regression model versus the calculated values by FAO-PM for Kashan station

Full size image
Fig. 10
figure 10

Comparison of the ET predicted with Bayesian regression model versus the calculated values by FAO-PM for Ardestan station

Full size image

To evaluate the Bayesian regression model, the amount of ET estimated by this model was plotted versus the calculated values. These results are shown for Esfahan, Kashan, and Ardestan stations in Figs. 8, 9, and 10, respectively. Similar to the robust regression analysis, the maximum value of the correlation coefficient was obtained for Ardestan; however, the minimum value of RMSE belongs to Kashan. It should be noted that performance of the Bayesian model for Kashan (Fig. 9) is the only overestimating observed in all models among all stations.

The formula obtained from Bayesian regression model for Esfahan, Kashan, and Ardestan stations are shown in Eqs. 18, 19, and 20, respectively.

$${\text{ET}} = - 20.2773 + 0.0769{\text{Ra}} - 0.7886(T_{\hbox{max} } - T_{\hbox{min} } ) + 2.7749T_{\text{mean}}$$
(18)
$${\text{ET}} = - 61.0469 + 0.0961{\text{Ra}} + 0.9314(T_{\hbox{max} } - T_{\hbox{min} } ) + 2.2568T_{\text{mean}}$$
(19)
$${\text{ET}} = - 87.9839 + 0.1166{\text{Ra}} + 2.4713(T_{\hbox{max} } - T_{\hbox{min} } ) + 4.0873T_{\text{mean}}$$
(20)

According to Tables 2, 3, and 4, the best results obtained from the MFP model with the highest regression coefficient and the lowest RMSE. The MFP model is more flexible than the ordinary polynomial methods and more resistant than nonparametric regression methods.

Figures 11 and 12 are plotted to better comparison of the performance of the models used with respect to the average values of the evaluation indices.

Fig. 11
figure 11

Comparison of the models used according to the average of the evaluation indices

Full size image
Fig. 12
figure 12

Comparison of the average of evaluation indices for area studies

Full size image

According to Fig. 11, once again the MFP model is introduced as the best model for estimation of reference ET in the study areas due to the highest correlation coefficient and the lowest RMSE and slope error. It should be noted that the slope error was obtained based on the coefficient of the suggested equations in Figs. 2, 3, 4, 5, 6, 7, 8, 9, and 10.

According to Fig. 12, the models used estimate reference ET in Kashan better than Esfahan and Ardestan. Table 1 confirms this result because the annual precipitation of Kashan (138.4 mm) is more than both Esfahan (122.8 mm) and Ardestan (115.8 mm). In addition, compared with Esfahan (1550.4 masl) and Ardestan (1252.4 masl), the lowest elevation belongs to Kashan (982.3 masl). Therefore, application of the models is proposed for all regions in the world with weather conditions close to Kashan, and this leads to the best performance as well as reduction of uncertainty for estimation of reference ET.

Compared with the previous works (in these three regions), the obtained results underline better performance of MFP, robust regression, and Bayesian regression in Esfahan, Kashan, and Ardestan. Azizi et al. (2010) applied multivariations regression model for estimating reference ET in Esfahan province. The authors used four weather parameters (temperature, air vapor pressure, relative humidity, and wind speed) to estimate reference ET and claimed that use of this approach led to correlation coefficients equal to 0.998 and 0.992, in Esfahan and Kashan, respectively. In the other study, Heydari et al. (2013) evaluated different methods include Penman FAO, Blaney–Criddle, Linacre, Thorenthwaite, Hargreaves–Samani, Irmak, Turc, and Jensen–Haise in Ardestan, and then their results were compared with FAO-PM method. The results indicated that the Blaney–Criddle model is the most appropriate for this particular study area, with an average RMSE of 1.34 mm day−1 and MAE of 1.00 mm day−1 and a correlation coefficient of 0.952. The obtained results can be expanded for other arid regions with similar wheatear conditions.

Summary and conclusions

In this research, the capacity of different models for evapotranspiration prediction was investigated. Evapotranspiration is a complex and nonlinear phenomenon because it depends on several interacting climatological factors, such as temperature, humidity, wind speed, radiation, type, and growth stage of the crop (Jain et al. 2008; Ojha and Bhakar 2012; Valipour 2012a, b, 2013c, d, e, f, g, h, Valipour 2014b). The MFP model is an effective tool to model nonlinear systems. The obtained results of predictions are in good agreement with the calculated ET at all stations. The results showed that the accuracy of MFP model was greater than the other two models in estimation of the amount of ET. Namely, the MFP model has more regression coefficient values and the less prediction errors than the other two models. Therefore, the suggestion is that these models, especially the MFP, could apply for other climatic and hydrologic modeling.

One of the most important results of the current investigation is estimation of reference ET by using only two weather variables including temperature and radiation, with an acceptable accuracy. Therefore, the formulae obtained are preferred to (1) other models in which reference ET was estimated using only these to variables with a future error as well as (2) other models in which reference ET was estimated using more weather variables such as relative humidity, wind speed, elevation, and precipitation.