Skip to main content

Advertisement

SpringerLink
Log in

Fractional-order delayed predator–prey systems with Holling type-II functional response

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

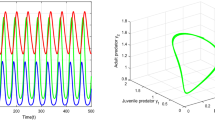
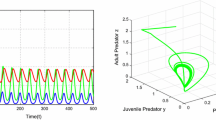
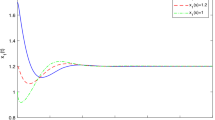
In this paper, a fractional dynamical system of predator–prey with Holling type-II functional response and time delay is studied. Local and global stability of existence steady states and Hopf bifurcation with respect to the delay is investigated, with fractional-order \(0< \alpha \le 1\). It is found that Hopf bifurcation occurs when the delay passes through a sequence of critical values. Unconditionally, stable implicit scheme for the numerical simulations of the fractional-order delay differential model is introduced. The numerical simulations show the effectiveness of the numerical method and confirm the theoretical results. The presence of fractional order in the delayed differential model improves the stability of the solutions and enrich the dynamics of the model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. We may notice that the characteristic equation of a system with delay has infinite roots.

  2. One definition of the stiffness is that the global accuracy of the numerical solution is determined by stability rather than local error, and implicit methods are more appropriate for it.

  3. Method of steps is not universal, as it cannot be applied with time-varying delays that vanish in some points.

References

  1. Ahmed, E., Hashish, A., Rihan, F.A.: On fractional order cancer model. J. Fract. Calc. Appl. 3(2), 1–6 (2012)

    Google Scholar 

  2. Anguelov, R., Lubuma, J.M.S.: Nonstandard finite difference method by nonlocal approximation. Math. Comput. Simul. 61, 465–475 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  3. Assaleh, K., Ahmad, W.M.: Modeling of speech signals using fractional calculus. In: 9th International Symposium on Signal Processing and Its Applications (ISSPA 2007) (2007)

  4. Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus Models and Numerical Methods. World Scientific, Singapore (2012)

    MATH  Google Scholar 

  5. Caponetto, R., Dongola, G., Fortuna, L.: Fractional Order Systems: Modeling and Control Applications. World Scientific, London (2010)

    Google Scholar 

  6. Chen, W.C.: Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fract. 36(5), 1305–1314 (2008)

    Article  Google Scholar 

  7. Cole, K.S.: Electric conductance of biological systems. In: Cold Spring Harbor Symposium on Quantitative Biology, pp. 107–116 (1993)

  8. Das, S., Gupta, P.: A mathematical model on fractional Lotka–Volterra equations. J. Theor. Biol. 277, 1–6 (2001)

  9. Debnath, L.: Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 54, 3413–3442 (2003)

    Article  MathSciNet  Google Scholar 

  10. Deng, W., Li, C., Lu, J.: Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 48, 409–416 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  11. Diethelm, K.: An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal. 5, 1–6 (1997)

    MATH  MathSciNet  Google Scholar 

  12. Diethelm, K., Ford, N., Freed, A.: A predictor–corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. Edelman, M.: Fractional maps as maps with power-law memory. In: Afraimovich, A., Luo, A.C.J., Fu, X. (eds.) Nonlinear Dynamics and Complexity, pp. 79–120. Springer, New York (2014)

    Chapter  Google Scholar 

  14. El-Sayed, A.: Nonlinear functional differential equations of arbitrary orders. Nonlinear Anal.: Theory Methods Appl. 33(2), 181–186 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  15. El-Sayed, A., El-Mesiry, A., El-Saka, H.: On the fractional-order logistic equation. Appl. Math. Lett. 20(7), 817–823 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  16. Ferdri, Y.: Some applications of fractional order calculus to design digital filters for biomedical signal processing. J. Mech. Med. Biol. 12(2), 13 (2012)

  17. Freedman, H.: Deterministic Mathematical Models in Population Ecology. Marcel Dekker, New York (1980)

    MATH  Google Scholar 

  18. Grahovac, N.M., Zigic, M.M.: Modelling of the hamstring muscle group by use of fractional derivatives. Comput. Math. Appl. 59, 1695–1700 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  19. Hilfer, R., Ed.: Applications of Fractional Calculus in Physics. World Scientific, River Edge (2000)

  20. Javidi, M., Nyamoradi, N.: Dynamic analysis of a fractional order prey–predator interaction with harvesting. Appl. Math. Model. 37, 8946–8956 (2013)

    Article  MathSciNet  Google Scholar 

  21. Laskin, N., Zaslavsky, G.M.: Nonlinear fractional dynamics on a lattice with long-range interactions. Phys. A 368, 38–54 (2006)

    Article  Google Scholar 

  22. Li, C., Zhang, F.: A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 193, 27–47 (2011)

    Article  Google Scholar 

  23. Li, L., Wang, Z.J.: Global stability of periodic solutions for a discrete predator–prey system with functional response. Nonlinear Dyn. 72, 507–516 (2013)

    Article  MATH  Google Scholar 

  24. Lin, W.: Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 332, 709–726 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  25. Lotka, A.: Elements of Physical Biology. Williams and Wilkins, Baltimore (1925)

    MATH  Google Scholar 

  26. Luo, A.C., (Eds.), V.A.: Long-Range Interaction, Stochasticity and Fractional Dynamics. New York, Springer (2010)

  27. Machado, J.A.T.: Analysis and design of fractional order digital control systems. Syst. Anal. Model. Simul. 27, 107–122 (1997)

  28. Machado, J.A.T.: Fractional-order derivative approximations in discrete-time control systems. Syst. Anal. Model. Simul. 34, 419–434 (1999)

  29. Machado, J.A.T.: Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 62(1–2), 371–378 (2010)

  30. Machado, J.A.T., Galhano, A.M.S.F.: Fractional order inductive phenomena based on the skin effect. Non-linear Dyn. 68(1–2), 107–115 (2012)

  31. Meng, X., Jiao, J., Chen, L.: The dynamics of an age structured predator–prey model with disturbing pulse and time delays. Nonlinear Anal.: Real World Appl. 9, 547561 (2008)

    MathSciNet  Google Scholar 

  32. Muth, E.: Transform Methods with Applications to Engineering and Operations Research. Prentice-Hall, New Jersey (1977)

    MATH  Google Scholar 

  33. Petras, I.: Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. HEP/Springer, London (2011)

    Google Scholar 

  34. Podlubny, I.: Fractional Differential Equations. Academic Press, London (1999)

    MATH  Google Scholar 

  35. Rihan, F.A.: Computational methods for delay parabolic and time fractional partial differential equations. Num. Meth. Partial Differ. Eqn. 26(6), 1556–1571 (2010)

    MATH  MathSciNet  Google Scholar 

  36. Rihan, F.A.: Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 11 (2013)

  37. Rihan, F.A., Abdelrahman, D.H.: Delay differential model for tumor-immune dynamics with HIV infection of CD4\(^{+}\) T-cells. Int. J. Comput. Math. 90(3), 594–614 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  38. Rihan, F.A., Abdelrahman, D.H., Lakshmanan, S.: A time delay model of tumour–immune system interactions: global dynamics, parameter estimation, sensitivity analysis. Appl. Math. Comput. 232, 606–623 (2014)

    Article  MathSciNet  Google Scholar 

  39. Rihan, F.A., Baleanu, D., Lakshmanan, S., Rakkiyappan, R.: On fractional SIRC model with salmonella bacterial infection. Abstr. Appl. Anal. 2014, 9 (2014)

  40. Rivero, M., Trujillo, J., Vazquez, L., Velasco, M.: Fractional dynamics of populations. Appl. Math. Comput. 218, 1089–1095 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  41. Sheng, H., Chen, Y.Q., Qiu, T.S.: Fractional Processes and Fractional-Order Signal Processing. Springer, New York (2012)

    MATH  Google Scholar 

  42. Suzuki, T.: A generalized banach contraction principle that characterizes metric completeness. Proc. Am. Math. Soc. 136(5), 1861–1869 (2008)

    Article  MATH  Google Scholar 

  43. Tang, G., Tang, S., Cheke, R.A.: Global analysis of a holling type II predator–prey model with a constant prey refuge. Nonlinear Dyn. 76, 635–664 (2014)

    Article  MathSciNet  Google Scholar 

  44. Tarasov, V.E.: Discrete map with memory from fractional differential equation of arbitrary positive order. J. Math. Phys. 50, 122,703 (2009)

    Article  MathSciNet  Google Scholar 

  45. Volterra, V.: Variazioni e fluttuazioni del numero di individui in specie animali conviventi

  46. Xia, Y., Cao, J., Cheng, S.: Multiple periodic solutions of a delayed stage-structured predator–prey model with non-monotone functional responses. Appl. Math. Model. 31, 1947–1959 (2007)

    Article  MATH  Google Scholar 

  47. Xu, H.: Analytical approximations for a population growth model with fractional order. Commun. Nonlinear Sci. Numer. Simul. 14, 1978–1983 (2009)

    Article  MATH  Google Scholar 

  48. Yuste, S.B., Acedo, L., Lindenberg, K.: Subdiffusion-limited A+B \(\rightarrow \) C reaction–subdiffusion process. Phys. Rev. E 69(3), 036,126 (2004)

    Article  Google Scholar 

  49. Zaslavsky, G.M.: Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 371, 461580 (2002)

    Article  MathSciNet  Google Scholar 

  50. Zaslavsky, G.M., Edelman, M., Tarasov, V.E.: Dynamics of the chain of forced oscillators with long-range interaction: from synchronization to chaos. Chaos 17(4), 043,124 (2007)

    Article  MathSciNet  Google Scholar 

  51. Zhang, J.F.: Bifurcation analysis of a modified Holling–Tanner predator–prey model with time delay. Appl. Math. Model. 36, 1219–1231 (2012)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was supported by NRF Grant Project (UAE University). Dr. R. Rakkiyappan was supported by DST SERB Project # SB/FTP/MS-045/2013. The authors thank Prof. J. A. Tenreiro Machado and referees for their valuable comments.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, College of Science, UAE University, Al-Ain, 15551, UAE

    F. A. Rihan & S. Lakshmanan

  2. Department of Physics, College of Science, UAE University, Al-Ain, 15551, UAE

    A. H. Hashish

  3. Department of Mathematics, Bharathiar University, Coimbatore, 641 046, India

    R. Rakkiyappan

  4. Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt

    E. Ahmed

Authors
  1. F. A. Rihan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Lakshmanan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. H. Hashish
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. Rakkiyappan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. E. Ahmed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. A. Rihan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rihan, F.A., Lakshmanan, S., Hashish, A.H. et al. Fractional-order delayed predator–prey systems with Holling type-II functional response. Nonlinear Dyn 80, 777–789 (2015). https://doi.org/10.1007/s11071-015-1905-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-1905-8

Keywords

Search

Navigation