Exit Time Distribution in Spherically Symmetric Two-Dimensional Domains

Abstract

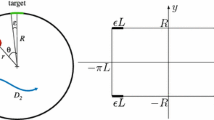
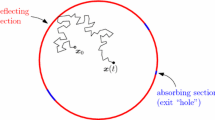
The distribution of exit times is computed for a Brownian particle in spherically symmetric two-dimensional domains (disks, angular sectors, annuli) and in rectangles that contain an exit on their boundary. The governing partial differential equation of Helmholtz type with mixed Dirichlet–Neumann boundary conditions is solved analytically. We propose both an exact solution relying on a matrix inversion, and an approximate explicit solution. The approximate solution is shown to be exact for an exit of vanishing size and to be accurate even for large exits. For angular sectors, we also derive exact explicit formulas for the moments of the exit time. For annuli and rectangles, the approximate expression of the mean exit time is shown to be very accurate even for large exits. The analysis is also extended to biased diffusion. Since the Helmholtz equation with mixed boundary conditions is encountered in microfluidics, heat propagation, quantum billiards, and acoutics, the developed method can find numerous applications beyond exit processes.

Appendices

Appendix 1: Simplification of $\alpha _{n}$ and $M_{nm}$

1.1 Simplified Expressions for $\alpha _{0}$

Herewith we prove the following identity for all $0 \le t < \pi$

$$\begin{aligned} \frac{\sqrt{2}}{\pi } \int _{0}^{t} \mathrm {d}x \frac{x \sin (x/2)}{\sqrt{\cos x - \cos t }} = - 2 \ln \left( \cos \left( \frac{t}{2}\right) \right) . \end{aligned}$$

(111)

We proceed by a change of variable $z = \cos x$ in the left-hand side term of Eq. (111) and we denote $T = \cos (t)$:

$$\begin{aligned} \int _{0}^{t} \mathrm {d}x \frac{x \sin (x/2)}{\sqrt{\cos x - \cos t }} = \int _{T}^{1} \mathrm {d}z \left[ \frac{\arccos z}{\sqrt{2\left( 1+z\right) }} \right] \frac{1}{\sqrt{z - T }}. \end{aligned}$$

(112)

We write the right-hand side of Eq. (111) in the form

$$\begin{aligned} - 2 \log \left( \cos \left( \frac{t}{2} \right) \right) = \log \left( \frac{2}{1+ T} \right) . \end{aligned}$$

(113)

From Ref. [15], the Abel’s equation

$$\begin{aligned} \int ^{1}_{T} \frac{y(z) \mathrm {d}z}{\sqrt{ z - T}} = \frac{\pi }{\sqrt{2}} \log \left( \frac{2}{1+ T} \right) \end{aligned}$$

(114)

has an unique solution for all $-1 < X < 1$

$$\begin{aligned} y(z) = \frac{1}{\pi } \frac{\pi }{\sqrt{2}} \int ^{z}_{1} \frac{\mathrm {d}u}{\sqrt{u -z}(1+z)} = \frac{\arccos {z}}{\sqrt{2 (1 + z)}}. \end{aligned}$$

(115)

Identification of the kernels of Eqs. (112) and (115) proves the identity (111).

The expression for $\alpha _{0}$ from Eq. (27a) is found by setting $t = \pi - \epsilon$ in Eq. (112). Note that the obtained expression for $\alpha _{0}$ from Eq. (27a) could also be deduced from the expression of the MFPT from Ref. [16].

1.2 Simplified Expressions for $\alpha _{n}, n \ge 1$

The solution of Eqs. (24a), (24b) is given in [8] in the form:

$$\begin{aligned} \alpha _{n} = \frac{1}{\sqrt{2} \pi } \int _{0}^{\pi - \epsilon }\! \! \! \mathrm {d}t \left( \frac{\partial }{\partial t} \int _{0}^{t} \mathrm {d}x \frac{x \sin (x/2)}{\sqrt{\cos x - \cos t }} \right) \bigl [ P_n(\cos t) + P_{n-1}(\cos t) \bigr ], \qquad n \ge 1. \end{aligned}$$

(116)

Using the identity (111), we show that

$$\begin{aligned} \alpha _{n} = \frac{1}{2} \int _{0}^{\pi - \epsilon } \! \! \! \mathrm {d}t \tan \left( \frac{t}{2}\right) \bigl [ P_n(\cos t) + P_{n-1}(\cos t) \bigr ], \qquad n \ge 1. \end{aligned}$$

(117)

After the change of variable $u = \cos t$, the latter identity leads to

$$\begin{aligned} \alpha _{n} = \frac{1}{2}\int ^{1}_{-\cos \epsilon } \frac{\mathrm {d}u}{1+u} \bigl [ P_n(u) + P_{n-1}(u)\bigr ] , \qquad n \ge 1. \end{aligned}$$

(118)

We now use the identity

$$\begin{aligned} \frac{\partial }{\partial x} \left( \frac{P_{m}(x)-P_{m-1}(x)}{m}\right) _{|x = X} = \frac{P_{m}(X) + P_{m-1}(X)}{1 + X}, \qquad m \ge 1, \end{aligned}$$

(119)

which is valid for all $X \in \left[ - 1 , 1 \right]$, to obtain the announced result:

$$\begin{aligned} \alpha _{n}&= \frac{(-1)^{n-1}}{2 n} \bigl [ P_{n}(\cos \epsilon ) + P_{n-1}(\cos \epsilon ) \bigr ] ,\qquad n \ge 1. \end{aligned}$$

(120)

1.3 Simplified Expression for $M_{nm}$

The expression for $M_{nm}$ from Eq. (46) can be simplified using Mehler’s integral representation (35):

$$\begin{aligned} M_{nm}&= \frac{1}{2} \int _{0}^{\pi - \epsilon } \! \! \! \mathrm {d}t \left\{ \frac{\partial }{\partial t} \left[ P_{m}(\cos t)-P_{m-1}(\cos t)\right] \right\} \bigl [ P_n(\cos t) + P_{n-1}(\cos t) \bigr ],\nonumber \\&\quad n \ge 1, \quad m \ge 1. \end{aligned}$$

(121)

The identity Eq. (119) then leads to the announced expression (47). Notice that the following matrix

$$\begin{aligned} S_{nm} = \sqrt{\frac{n}{m}}M_{nm}, \qquad n \ge 1, \quad m \ge 1, \end{aligned}$$

(122)

is symmetric. The eigenvalues of $S_{nm}$ are real, and so are the eigenvalues of $M$. In Sect. 5.5 we show that the coefficients $\alpha _n$ are given by an eigenvector of the infinite-dimensional matrix $M$.

1.4 Perturbative Expansion of $M_{nm}$

We first derive an alternative identity to Eq. (119). Let us define

$$\begin{aligned} A_n(x) \equiv \frac{\partial }{\partial x} (P_{n}(x) - P_{n-1}(x)), \qquad n \ge 1. \end{aligned}$$

(123)

Using the recurrence formulas for Legendre polynomials, we obtain

$$\begin{aligned} A_n(x)&= (P'_{n}(x) -P'_{n-2}(x))- (P'_{n-1}(x) -P'_{n-2}(x))\nonumber \\&= (2n-1)P_{n-1}(x) - A_{n-1}(x)= \sum ^{n}_{k=1} (-1)^{n-k} (2k-1)P_{k-1}(x), \end{aligned}$$

(124)

where we used $P_{0}(x) = 1$, $P_{1}(x) = x$, and $A_1(x) = 1 = (2-1) P_{0}(x)$.

Combining Eq. (121) and the identity (124) we obtain the announced result:

$$\begin{aligned} M_{nm}&= \int _{0}^{\pi - \epsilon } \! \mathrm {d}t \ \frac{\sin t}{2} A_m (\cos t) \bigl [ P_n(\cos t) + P_{n-1}(\cos t) \bigr ], \nonumber \\&= \sum ^{m}_{k=1} (-1)^{n-k} (2k - 1) \left( K_{k-1,n-1} + K_{k-1,n} \right) , \end{aligned}$$

(125)

where the coefficients $K_{k,n}$ are defined by

$$\begin{aligned} K_{k,n} \equiv \int _{0}^{\pi - \epsilon } \! \! \! \mathrm {d}t \ P_k(\cos t) P_n(\cos t) \frac{\sin t}{2}. \end{aligned}$$

(126)

In the leading order in $\epsilon \ll 1$, Eq. (125) reads

$$\begin{aligned} M_{nm} = \sum ^{m}_{k=1} (-1)^{n-k} (2k - 1) \left( \frac{\delta _{k-1,n-1}}{2n-1} + \frac{\delta _{k-1,n}}{2n+1} \right) + \mathcal {O}(\epsilon ). \end{aligned}$$

(127)

If $m < n$, it is straightforward to show that $M_{nm} = \mathcal {O}(\epsilon )$. If $m > n$, $M_{nm} = \mathcal {O}(\epsilon )$ as successive terms with $k = n$ and $k = n +1$ cancel each other. The matrix $M_{nm}$ ($n,m \ge 1$) is thus diagonal at the first order in $\epsilon$:

$$\begin{aligned} M_{nm} = \delta _{nm} + \mathcal {O}(\epsilon ). \end{aligned}$$

(128)

In order to get the next term in the series expansion in $\epsilon \ll 1$, we write

$$\begin{aligned} M_{nm} - \delta _{nm}&= - \frac{m}{2} \int ^{-\cos \epsilon }_{-1} \frac{1}{1+x} \bigl [ P_m(x)+P_{m-1}(x) \bigr ] \bigl [ P_n(x)+P_{n-1}(x) \bigr ] \mathrm {d}x,\nonumber \\&\quad n \ge 1, \quad m \ge 1. \end{aligned}$$

(129)

We now focus on the term in the right-hand side of Eq. (129). In the vicinity of $x = -1$, the integrand of Eq. (129) expands into

$$\begin{aligned} \frac{1}{1+x} \bigl [ P_m(x)+P_{m-1}(x) \bigr ] \bigl [ P_n(x)+P_{n-1}(x) \bigr ] = \frac{nm (-1)^{n+m}}{8} (1 +x)+ \mathcal {O}(1+x). \end{aligned}$$

(130)

Notice that

$$\begin{aligned} \int ^{-\cos \epsilon }_{-1} (1 + x) \mathrm {d}x = \frac{\epsilon ^4}{8} + \mathcal {O}(\epsilon ^5). \end{aligned}$$

(131)

Substituting Eqs. (130) and (131) into Eq. (129) leads to

$$\begin{aligned} M_{nm} = \delta _{mn} + \frac{nm^2 (-1)^{n+m}}{8} \epsilon ^4 + \mathcal {O}(\epsilon ^5). \end{aligned}$$

(132)

1.5 Summation Identities

Using the identities for sums of Legendre polynomials from Ref. [37], we derive the following equation

$$\begin{aligned} S&\equiv \sum ^{\infty }_{m = 1} (-1)^{m-1} \bigl [ P_{m}(\cos x) + P_{m-1}(\cos x) \bigr ] \bigl [ P_{m}(\cos \epsilon ) + P_{m-1}(\cos \epsilon ) \bigr ] = 2,\nonumber \\&\quad 0 < x < \pi - \epsilon . \end{aligned}$$

(133)

To prove this identity, we first use the Mehler’s representation (35) for Legendre polynomials $P_{m}(\cos \epsilon )$ and $P_{m-1}(\cos \epsilon )$ to obtain

$$\begin{aligned} S&= \frac{2}{\pi } \int ^{\pi - \epsilon }_{0} \frac{ \sum ^{\infty }_{m = 1} \bigl [ P_{m}(\cos x) + P_{m-1}(\cos x) \bigr ] \left[ \cos (\left( m + \frac{1}{2}\right) t)- \cos (\left( m - \frac{1}{2}\right) t)\right] }{ \sqrt{(\cos (t)+\cos \epsilon )(\cos x- \cos (t))} },\nonumber \\&\quad 0 < x < \pi . \end{aligned}$$

(134)

We then use trigonometric identities and the series identity (39) to obtain the following integral representation

$$\begin{aligned} S = -\frac{2}{\pi } \int ^{\pi - \epsilon }_{x} \! \! \! \mathrm {d}t \frac{2 \sin \left( \frac{t}{2}\right) \cos \left( \frac{t}{2}\right) }{\sqrt{(\cos (t)+\cos \epsilon )(\cos x- \cos (t))}}, \qquad 0 < x < \pi - \epsilon . \end{aligned}$$

(135)

The consecutive change of variables $z = \cos (t)$ and $U = \sqrt{(z+\cos \epsilon )(\cos x- z)}$ leads to

$$\begin{aligned} S = \frac{2}{\pi } \int ^{\cos x}_{-\cos x} \frac{\mathrm {d}z}{\sqrt{(z+\cos \epsilon )(\cos x- z)}} = 2, \end{aligned}$$

(136)

which proves the identity (133). We will use this identity in the following form:

$$\begin{aligned} \sum ^{\infty }_{m = 1} \bigl [ P_{m}(\cos x) + P_{m-1}(\cos x) \bigr ] m \ \alpha _m = 1, \qquad 0 < x < \pi - \epsilon . \end{aligned}$$

(137)

where $\alpha _m$ are given by Eq. (27b).

1.5.1 Proof of the Identity (83)

We write $\alpha _m$ from Eq. (25b) and exchange the sum and the integral to obtain:

$$\begin{aligned} \sum ^{\infty }_{m=1} 2 m \alpha ^2_m&= \frac{\sqrt{2}}{\pi } \int _{0}^{\pi - \epsilon } \! \! \! \mathrm {d}t \left( \frac{\partial }{\partial t} \int _{0}^{t} \mathrm {d}x \frac{x \sin (x/2)}{\sqrt{\cos x - \cos t }} \right) \nonumber \\&\quad \times \left( \sum ^{\infty }_{m=1} \bigl [ P_m(\cos t) + P_{m-1}(\cos t) \bigr ] m \alpha _m \right) . \end{aligned}$$

(138)

Using the identity (133) in the right-hand side of Eq. (138) and the representation (25a) of $\alpha _0$ leads to the result of Eq. (83).

1.5.2 An Eigenvector of the Matrix $M$

We show that the coefficients $\alpha _n$ (with $n \ge 1$) form an eigenvector of the matrix $M$:

$$\begin{aligned} \sum ^{\infty }_{m=1} M_{nm} \alpha _m= \alpha _n. \end{aligned}$$

(139)

We express $M_{nm}$ through Eq. (47) and exchange the sum and the integral:

$$\begin{aligned} \sum ^{\infty }_{m=1} M_{nm} \alpha _m&= \frac{1}{2} \int ^{1}_{-\cos \left( \epsilon \right) } \frac{1}{1+x} \left( P_n(x)+P_{n-1}(x)\right) \nonumber \\&\quad \times \left( \sum ^{\infty }_{m=1} \bigl [ P_m(\cos t) + P_{m-1}(\cos t) \bigr ] m \alpha _m \right) \mathrm {d}x, \end{aligned}$$

(140)

from which the identity (133) leads to the announced identity (139).

Appendix 2: Spatially Averaged Variances

We denote by $\overline{\mathbb {E}\left[ \tau ^n\right] }$ the spatial average of the $n$th moment of the exit time:

$$\begin{aligned} \overline{\mathbb {E}\left[ \tau ^n\right] } \equiv \dfrac{1}{\pi } \int _{\vec {r}_0 \in \Omega } \! \! \! \mathrm {d} \vec {r}_0 \ \mathbb {E}\left[ \tau ^n_{\vec {r}_0}\right] , \end{aligned}$$

(141)

where $\mathrm {d} \vec {r}_0$ is the uniform measure over $\Omega$. Let us now consider the random variable $\tau _{\Omega }$, defined in Sect. 2.4.1 as the exit time of a particle started at a random starting position $X$. The $n$th moment $\tau _{\Omega }$ reads

$$\begin{aligned} \mathbb {E}\left[ \tau _{\Omega }^n\right] \equiv \int _{\vec {r}_0 \in \Omega } \! \! \! \mathrm {d}\mu (X = \vec {r}_0) \mathbb {E}\left[ \tau _{X}^n\right] , \end{aligned}$$

(142)

where $\mathrm {d} \mu (X =\vec {r}_0)$ is the probability density for $X$ to be started at the position $\vec {r}_0$. If $\mathrm {d} \mu (X =\vec {r}_0) =\mathrm {d} \vec {r}_0$ is the uniform probability distribution, we can identify Eqs. (141) and (142), $\mathbb {E}\left[ \tau _{\Omega }^n\right] = \overline{\mathbb {E}\left[ \tau ^n\right] }$, and the variance of the random variable $\tau _{\Omega }$ is

$$\begin{aligned} \mathrm {Var}\left[ \tau _{\Omega } \right] \equiv \left( \int _{\vec {r}_0 \in \Omega } \! \mathrm {d}\mu (X = \vec {r}_0) \mathbb {E}\left[ \tau _X^2\right] \right) - \left( \int _{\vec {r}_0 \in \Omega } \! \mathrm {d}\mu (X= \vec {r}_0) \mathbb {E}\left[ \tau _X\right] \right) ^2 = \overline{\mathbb {E}\left[ \tau ^2\right] } - \overline{\mathbb {E}\left[ \tau \right] }^2. \end{aligned}$$

(143)

Note that $\mathrm {Var}\left[ \tau _{\Omega } \right]$ differs from the spatial average of the variance: $\mathrm {Var}\left[ \tau _{\Omega } \right] \ne \overline{\mathrm {Var}\ \tau } = \overline{\mathbb {E}\left[ \tau ^2\right] } - \overline{\mathbb {E}\left[ \tau \right] ^2}$, because $\overline{\mathbb {E}\left[ \tau \right] }^2 \ne \overline{\mathbb {E}\left[ \tau \right] ^2}$.

Appendix 3: Convergence to an Exponential Distribution in the Narrow-Escape Limit

1.1 From the Expression for the Survival Distribution

We recall that the expressions for $(\alpha _n), n \ge 0,$ in the limit $\epsilon \ll 1$ are provided in Eqs. (59a)–(59b). We denote by $\tilde{S}_{e}(t)$ the normalized single exponential distribution whose mean is equal to the GMFPT defined in Eq. (13). The Laplace transform of the distribution $\tilde{S}^{(t)}_{e}$ is

$$\begin{aligned} S^{(p)}_{e} = \dfrac{\overline{\mathbb {E}\left[ \tau \right] }}{1 + p \ \overline{\mathbb {E}\left[ \tau \right] }}. \end{aligned}$$

(144)

We show that in the narrow-escape limit ($\epsilon \ll 1$), the averaged exit time distribution $\overline{S^{(p)}} \approx a^{(p)}_0/2$ converges to $S_{e}^{(p)}$, as expected from Ref. [12]. Due to the divergence of the coefficient $\alpha _0$ from Eq. (59a), the asymptotic expansion of Eq. (52a) at the first order in $\epsilon \ll 1$ reads

$$\begin{aligned} \frac{a_{0}^{(p)}}{2} = \alpha _0 \left[ \partial _r f^{[1]}_{0}\right] _{|r=1} \left[ \sum ^{\infty }_{k = 0} \left( p \left[ \partial _r f^{[1]}_{0}\right] _{|r=1} \alpha _0\right) ^k \right] + \mathcal {O}(\epsilon ). \end{aligned}$$

(145)

where $\left[ \partial _r f^{[1]}_{0}\right] _{|r=1}$ is the first-order expansion in $p \ll 1$ of $\left[ \partial _r f^{(p)}_{0}\right] _{|r=1}$. At the leading order in $\epsilon$, the averaged survival probability over $\Omega$ is

$$\begin{aligned} \overline{S^{(p)}} = \frac{\alpha _0 \left[ \partial _r f^{[1]}_{0}\right] _{|r=1} }{1 + \alpha _0 \left[ \partial _r f^{[1]}_{0}\right] _{|r=1} } + \mathcal {O}(\epsilon ). \end{aligned}$$

(146)

Combining Eqs. (21) and (52a), the GMFPT at the leading order in $\epsilon \ll 1$ is

$$\begin{aligned} \overline{\mathbb {E}\left[ \tau \right] } = \alpha _{0} \left[ \partial _r f^{[1]}_{0}\right] _{|r=1} + \mathcal {O}(\epsilon ). \end{aligned}$$

(147)

Combining Eqs. (144) and (146) leads to

$$\begin{aligned} \overline{S^{(p)}} = \overline{S^{(p)}_{e}} + \mathcal {O}(\epsilon ). \end{aligned}$$

(148)

This shows the convergence in law of the FPT distribution to an exponential distribution whose mean is the GMFPT as expected for the narrow-espace limit [12].

1.2 From the Expression for the Moments

Let us consider the random variable $\tau _{\Omega }$, defined in Sect. 2.4.1 as the exit time of a particle started at a random starting position. We provide a positive answer to the following question: does the distribution of $\tau _{\Omega }$ converge to an exponential distribution in the limit $\epsilon \ll 1$, even though the starting positions within the boundary layer contribute to the statistics of $\tau _{\Omega }$? Using the recurrence scheme of Sect. 2.4.1, we verify that at the leading order in $\epsilon \ll 1$ the moments of $\tau _{\Omega }$ are

$$\begin{aligned} \mathbb {E}\left[ \tau _{\Omega }^n\right] = n! \left( \frac{\alpha _0}{2}\right) ^n + \mathcal {O}(\ln (\epsilon )^{n-1}), \end{aligned}$$

(149)

which leads to $\mathbb {E}\left[ \tau _{\Omega }^n\right] = n! \ \mathbb {E}\left[ \tau _{\Omega }\right] ~ (n \ge 1)$ at the leading order in $\epsilon$. The latter identity indicates that the FPT distribution of $\tau _{\Omega }$ converges to an exponential distribution whose mean is the GMFPT defined by Eq. (29), as expected from Sect. 7.1. We emphasize that the relation $\mathbb {E}\left[ \tau _{\Omega }^n\right] = n! \ \mathbb {E}\left[ \tau _{\Omega }\right] ~ (n\ge 1)$, implies that the GMFPT characterizes the whole distribution of the exit time, in contrast to the statement of Eq. (18) from Ref. [18].

Appendix 4: Computational Aspects

We summarize the numerical methods used to compute the FPT distribution.

• (i) The Monte Carlo simulations rely on a sample of $2 \cdot 10^{6}$ of random walks. This sample is obtained through $2$ hours of computation on $200$ CPUs ($3.20$ GHz Intel Core$^\mathrm{TM}$ i7). The home-built C++ program uses an adaptive time step method so that the time steps are given by a decreasing function with the distance to the exit.

• (ii) A finite element method realized in COMSOL Multiphysics v4.2 [33] allowed to greatly reduce the computational time. For instance, the FPT probability density shown in Fig.2a, b required 10–15 min on a single CPU ($2,66$ GHz Intel Core $^\mathrm{TM}$ i5).

• (iii) The exact and approximate analytical solutions were computed in MATLAB and using the numerical Laplace inversion package INVLAP [38]. The series were truncated at $N = 100$ terms and the computational time is of the order of a few minutes on a single CPU ($2,66$ GHz Intel Core $^\mathrm{TM}$ i5).