Kinetics of Active Surface-Mediated Diffusion in Spherically Symmetric Domains

Abstract

We present an exact calculation of the mean first-passage time to a target on the surface of a 2D or 3D spherical domain, for a molecule alternating phases of surface diffusion on the domain boundary and phases of bulk diffusion. We generalize the results of Bénichou et al. in (J. Stat. Phys. 142:657, 2011) and consider a biased diffusion in a general annulus with an arbitrary number of regularly spaced targets on a partially reflecting surface. The presented approach is based on an integral equation which can be solved analytically. Numerically validated approximation schemes, which provide more tractable expressions of the mean first-passage time are also proposed. In the framework of this minimal model of surface-mediated reactions, we show analytically that the mean reaction time can be minimized as a function of the desorption rate from the surface.

Appendices

Appendix A: Boundary Condition for the MFPT

We check that Eq. (4) giving the discontinuity relation of the MFPT between the semi-reflecting surface and the bulk can be derived either from a discrete lattice model or from a standard forward equation on conditional probabilities [4, 46].

1.1 A.1 A Discrete Lattice Approach

Let us first consider a 2D geometry in which the bulk and surface states are two lattices with radial and angular steps Δr and Δθ. The circular geometry imposes the relation on the radial and angular steps in the bulk at the radius r: Δr(r)=rΔθ. At each time step Δt, the molecule moves to one of its closest neighboring sites. The value of the time step is adjusted according to the position of the molecule:

$$ \varDelta t (i,r) = \sqrt{r \varDelta \theta} / D_{i} , $$

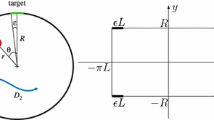
where i=1 for the molecule on the adsorbing surface and i=2 for the molecule in the bulk. This choice maintains in the continuous limit a spatially constant value for the diffusion coefficient D ₂. At r=R, a molecule may either (i) get reflected to r=R−Δr with probability q/2, (ii) get adsorbed onto the surface with probability (1−q)/2, (iii) move along the angular direction, with probability 1/2 (see Fig. 11). Let the random variable τ ₂(r,θ) (resp. τ ₁(θ)) denote the first passage time (FPT) for a molecule initially in the bulk at (r,θ) (resp., on the surface at θ). The probability for τ ₂(r,θ) to be t=mΔt (m∈ℕ), is equal to an average of the probabilities of the FPT from neighboring sites to be (m−1)Δt:

(71)

The mean FPT in the discrete lattice model is defined as

$$ t_{2}(r,\theta) \equiv\sum ^{\infty}_{m=1} m \; \varDelta t \;\mathbb{P} \bigl\{ \tau_{2}(r,\theta)= m \varDelta t \bigr\}. $$

(72)

Combining this definition with Eq. (71) leads to

$$ t_{2}(R,\theta) = \frac{q}{2} \; t_{2}(R - \varDelta r, \theta) + \frac {1-q}{2} \; t_{1}(\theta) + \frac{1}{4} \bigl( t_{2}(R, \theta+ \varDelta \theta) + t_{2}(R, \theta- \varDelta \theta) \bigr) + \varDelta t. $$

The Taylor expansion of t ₂(R,θ) gives

(73)

Following [46, 47], the adsorption coefficient is defined as

$$ k \equiv\frac{1-q}{q}\frac{1}{R \varDelta \theta}. $$

(74)

In the continuous limit, when all $\varDelta r,\; \varDelta \theta, \; \varDelta t$ tend to 0 with Δr/Δθ=r and D ₂≡Δr ²/(2Δt) constant, Eq. (73) turns out to be expressed in terms of k only:

$$ \frac{\partial t_{2}}{\partial r}_{|{\mathbf{r}}=(R,\theta)} = k \bigl( t_{1}(\theta) - t_{2}(R,\theta) \bigr) + o(1). $$

(75)

Indeed Δt/Δr=o(1) and Δθ ²/Δr=o(1) in this limit. For a perfectly adsorbing boundary we have q=0, k→∞, which is indeed compatible with the continuity relation t ₂(R,θ)=t ₁(θ) used in Ref. [1]. For a perfectly reflecting boundary q=1, k→0 and ∂ _r t ₂(r,θ)=0 at r=R [4]. This is indeed the condition that we imposed on the boundary r=R _c in Sect. 3.

Fig. 11

A discrete lattice model. Regular Δθ slicing imposes Δt and Δr to vary over the domain S in order to maintain an isotropic diffusion constant D ₂. Only one quadrant is presented

1.2 A.2 Equivalence with a Forward Boundary Condition

We now check that the MFPT condition of Eq. (4) is also compatible with the following boundary condition on the conditional probability [4]

(76)

where p(x,t|x′,t′) is the probability for a molecule to be at x at time t provided that the molecule was at x′ at an earlier time t′<t. We denote the spatial coordinate x=(r,θ) if the molecule is in the bulk and x=θ if it is adsorbed on the surface.

We follow the standard method presented in [46]. The stochastic process under study is Markovian hence the conditional probabilities satisfy the Chapman-Kolmogorov equation, with t>s>t′,

where S=(R,R _c )×[0,π] and the measure dν is

Taking the derivative with respect to the intermediate time s leads to the expression

(77)

The backward Chapman-Kolmogorov equations read

(78)

(79)

The forward Chapman-Kolmogorov equations are

(80)

(81)

The terms in Eqs. (80) and (81) are justified as follows: (i) −λ p(θ,s|x′,t′) corresponds to a constant rate of desorption from the surface to the bulk; (ii) −D ₂ ∂ _r p((r,θ),s|x′,t′) is the flux into the surface due to diffusion; (iii) is the flux into the surface due to the drift (by convention, v(R)>0 for a velocity drift field oriented towards to the exterior); (iv) corresponds to the flux into the bulk due to the desorption from the surface and the ejection at a distance a (δ being the Dirac delta function).

For convenience, we will use the shorthand notations p(y,s|x′,t′)≡p(y), and p(θ,s|x′,t′)≡p(θ). Substituting the Chapman-Kolmogorov equations (78)–(81) into Eq. (77) leads to the following equation

One notices that

and that the four terms proportional to λ vanish. Two terms with angular Laplacians also cancel each other due to the hermiticity of the angular diffusion operator:

The divergence theorem yields the integral over the frontier ∂S of the annulus S:

This equality can be satisfied only if:

$$ \frac{\partial\bar{p}((r,\theta),s)}{\partial r}_{|r= R} \; p\bigl((R,\theta),s \bigr) = \frac{\partial p((r,\theta),s)}{\partial r}_{|r= R} \bigl[ \bar{p}\bigl((r,\theta),s \bigr) - \bar{p}(\theta,s) \bigr]. $$

(82)

Inserting the forward boundary condition (76) into Eq. (82) gives the boundary condition on the backward probability distribution

Integrating over the space and time variables x and t, we obtain the boundary condition for the MFPT:

$$ \frac{\partial t_{2}}{\partial r}_{|{\mathbf{r}}= (R,\theta)} = k \bigl\{ t_{1}(\theta) - t_{2}(R,\theta) \bigr\} \qquad(0\leq\theta\leq\pi), $$

which identifies with Eq. (4).

Appendix B: Interpretation of η _d /D ₂ as a Mean First Passage Time

We consider the probability density $\varPi(\tilde{\theta}|\theta)$ for a molecule initially at the bulk point (R−a,θ) to first reach the surface r=R at the angle $\tilde{\theta}$. The mean duration of this Brownian path is denoted $t_{c}(\tilde{\theta}|\theta)$.

The MFPT t ₂(R−a,θ) to reach the target can be expressed as the averaged sum of the MFPT to reach a point $(R,\tilde{\theta})$ on the surface and the MFPT to reach the target from this point of the surface, the probability density for the first hitting point $(R,\tilde{\theta })$ being the harmonic measure $\varPi(\tilde{\theta}|\theta)$:

$$ t_{2}(R-a,\theta) = \int^{\pi}_{0} \bigl( t_{c}(\tilde{\theta}|\theta) + t_{1}(\tilde{\theta}) \bigr) \varPi(\tilde{\theta}|\theta) d\mu_d(\tilde{\theta}). $$

(83)

In 2D and in the general case considered in Sect. 3, the probability density $\varPi(\tilde{\theta}|\theta)$ is

$$ \varPi(\tilde{\theta}|\theta) = 1 + 2 \sum^{\infty}_{n=1} (X_{n}+1) \cos\bigl( n (\tilde{\theta}-\theta)\bigr), $$

(84)

where X _n is given by Eq. (25). Substitution of this expression in Eq. (83) leads to

(85)

Identification with Eq. (36) gives

$$ \frac{\eta_{d}}{D_2} = \frac{1}{\pi} \int ^{\pi}_{0} t_{c}(\tilde{\theta}|\theta) \varPi(\tilde{\theta}|\theta) d\tilde{\theta}= \frac{1}{\pi} \int ^{\pi}_{0} t_{c}(\tilde{\theta}|0) \varPi(\tilde{\theta}|0) d\tilde{\theta}, $$

(86)

which identifies η _d /D ₂ as the MFPT to the circle of radius R. In particular, it can be shown that in the 2D case of Sect. 4.1.1

$$ \varPi(\tilde{\theta}|\theta) t_{c}(\tilde{\theta}|\theta) = \frac {R^2}{4 D_2} \bigl( 1 - (r/R)^2 \bigr) \Biggl( 1 + \sum ^{\infty}_{n=1} \frac{(r/R)^n}{2 (1+n)} \cos\bigl(n ( \theta-\tilde{\theta})\bigr) \Biggr). $$

(87)

One can verify that the substitution of this expression into Eq. (86) leads to the well known result of Eq. (47), η ₂=R ²(1−x ²)/4.

The argument leading to Eq. (86) can be extended to the 3D case with the following expression for the probability density:

$$ \varPi(\tilde{\theta}|\theta) = 1 + \sum^{\infty}_{n=1} (2n+1) (X_{n}+1) P_{n}(\cos{\tilde{\theta}}) P_{n}(\cos{\theta}). $$

(88)

Appendix C: Matrix Elements I _ϵ (n,m) in 3D

The matrix elements I _ϵ (n,m) in 3D were computed in [1]. An explicit formula for non-diagonal elements (m≠n) is given in Table 1. In turn, the diagonal elements I _ϵ (n,n) can be expressed as

$$ I_\epsilon(n,n) = - P_n(u) \frac{u P_n(u) - P_{n-1}(u)}{n+1} + \frac {F_n(u) + 1}{2n+1}, \quad u = \cos\epsilon, $$

through the function F _n (u), for which the explicit representation was derived in [1]

(89)

One can also check that this function satisfies the recurrence relations

$$ F_n(u) = F_{n-1}(u) + u\bigl[P_n^2(u) + P_{n-1}^2(u)\bigr] - 2P_n(u) P_{n-1}(u) , \qquad F_0(u) = u . $$

(90)

that simplifies its numerical computation. Note that F _n (±1)=F _n−1(±1)=⋯=±1.

Appendix D: Case of a 1/r ² Velocity Field

We now examine the 3D case of a radial 1/r ² velocity field $\vec{v}(r)$, which is characterized by the dimensionless parameter μ:

$$ \vec{v}(r) = -\frac{\mu D_{2} R}{r^3} \; \vec{r}. $$

(91)

The function $\hat{f}$ is expressed as

$$ \hat{f}(r) = -\frac{r^2}{6} - \frac{r R \mu}{6} + \frac{R^2 \mu^2}{6} e^{-\mu R/r} \mathrm{Ei}(\mu R/r), $$

(92)

where Ei(z) is the exponential integral:

$$ \mathrm{Ei}(z) = \int _{-\infty}^z \frac{e^x}{x} dx . $$

The function f ₀ is

$$ f_{0}(r) = \frac{1 - e^{-\mu R/r}}{\mu} $$

(93)

(this particular choice of the additive and multiplicative constants ensures that R/r is retrieved in the limit μ→0). Radial functions f _n (r) are found as products of powers and confluent hypergeometric functions ₁ F ₁ of r:

(94)

(95)

For n=0, this expression is reduced to e ^−μR/r. In the limit μ→0, the above functions reduce to r ⁿ and r ⁻ⁿ⁻¹ from the earlier case μ=0. On the one hand we have

from which

$$ \frac{\partial_r f_{n}(r)}{\partial_r f_{-n}(r)} = - \frac{n}{n+1} r^{2n+1} \frac{_{1}F_{1}(-n+1,\; -2n,\; -\mu R/r)}{ _{1}F_{1}(n+2,\; 2n+2,\; -\mu R/r)}. $$

(96)

On the other hand we have

from which

$$ \frac{\partial_r \hat{f}(r)}{\partial_r f_0(r)} = -\frac{\mu}{6} \bigl[(\mu R)^2 \mathrm{Ei}(\mu R/r) - e^{\mu R/r} \bigl[\mu R r + r^2 - 2r^3/(\mu R) \bigr] \bigr] . $$

(97)

This last expression is needed to compute the quantities η _d and X _n .