Abstract
The molecular structure of \(\upalpha\)-l-Rhap-(1→ 2)-\(\upalpha\)-l-Rhap-OMe has been investigated using conformation sensitive NMR parameters: cross-relaxation rates, scalar 3 J CH couplings and residual dipolar couplings obtained in a dilute liquid crystalline phase. The order matrices of the two sugar residues are different, which indicates that the molecule cannot exist in a single conformation. The conformational distribution function, \(P(\upphi,\uppsi)\), related to the two glycosidic linkage torsion angles \(\upphi\) and \(\uppsi\) was constructed using the APME method, valid in the low orientational order limit. The APME approach is based on the additive potential (AP) and maximum entropy (ME) models. The analyses of the trajectories generated in molecular dynamics and Langevin dynamics (LD) computer simulations gave support to the distribution functions constructed from the experimental NMR parameters. It is shown that at least two conformational regions are populated on the Ramachandran map and that these regions exhibit very different molecular order.
Similar content being viewed by others
Abbreviations
- R2R:
-
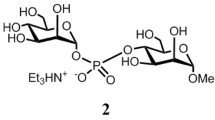
\(\upalpha\)-l-Rhap-(1→ 2)-\(\upalpha\)-l-Rhap-OMe
- RDC:
-
residual dipolar couplings
References
Berardi R., Spinozzi F., Zannoni C. (1998). J. Chem. Phys. 109: 3742–3759
Berendsen H.J.C., Postma J.P.M., van Gunsteren W.F., DiNola A., Haak J.R. (1984). J. Chem. Phys. 81: 3684–3690
Brink D.M., Satchler G.R. (1993) Angular Momentum. Clarendon Press, Oxford
Brooks B.R., Bruccoleri R.E., Olafson B.D., States D.J., Swaminathan S., Karplus M. (1983). J. Comput. Chem. 4:187–217
Castellani F., van Rossum B., Diehl A., Schubert M., Rehbein K., Oschkinat H. (2002). Nature 420: 98–102
Catalano D., Di Bari L., Veracini C.A., Shilstone G.N., Zannoni C. (1991). J. Chem. Phys. 94: 3928–3935
Cloran F., Carmichael I., Serianni A.S. (1999). J. Am. Chem. Soc. 121: 9843–9851
Delaglio F., Grzesiek S., Vuister G.W., Zhu G., Pfeifer J., Bax A. (1995). J. Biomol. NMR 6: 277–293
Delaglio F., Wu Z., Bax A. (2001). J. Magn. Reson. 149: 276–281
Eklund R., Widmalm G. (2003). Carbohydr. Res. 338: 393–398
Emsley J.W., Luckhurst G.R., Stockley C.P. (1982). Proc. R. Soc. Lond. A 381: 117–138
Fung B.M. (2002). Prog. Nucl. Magn. Reson. Spectrosc. 41: 171–186
Hardy B.J., Bystricky S., Kovac P., Widmalm G. (1997). Biopolymers 41: 83–96
Hockney R.W. (1970). Meth. Comput. Phys. 9: 136–211
Jansson P.-E., Kenne L., Widmalm G. (1991). Acta Chem. Scand. 45: 517–522
Keepers J.W., James T.L.J. (1984). Magn. Reson. 57: 404–426
Kjellberg A., Widmalm G. (1999). Biopolymers 50: 391–399
Kroon-Batenburg L.M.J., Kroon J., Leeflang B.R., Vliegenthart J.F.G. (1993). Carbohydr. Res. 245: 21–42
Lemieux R.U., Koto S. (1974). Tetrahedron 30: 1933–1944
Loncharich R.J., Brooks B.R., Pastor R.W. (1992). Biopolymers 32: 523–535
Lycknert K., Helander A., Oscarson S., Kenne L, Widmalm G. (2004). Carbohydr. Res. 339: 1331–1338
MacKerell Jr. A.D., Bashford D., Bellott M., Dunbrack Jr. R.L., Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kushnir L., Kuczera K., Lau F.T.K., Mattos C., Michnick S., Ngo T., Nguyen T.D., Prodhom B., Reiher III W.E., Roux B., Schlenkrich M., Smith J.C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., Karplus M. (1998). J. Phys. Chem. B 102: 3586–3616
Merlet D., Emsley J.W., Lesot P., Courtieu J. (1999). J. Chem. Phys. 111: 6890–6896
Norberg T., Oscarson S., Szönyi M. (1986). Carbohydr. Res. 156: 214–217
O’Neil-Cabello E., Bryce D.L., Nikonowicz E.P., Bax A. (2004). J. Am. Chem. Soc. 126: 66–67
Otting G., Rückert M., Levitt M.H., Moshref A. (2000). J. Biomol. NMR 16: 343–346
Prestegard J.H., Al-Hashimi H.M., Tolman H.M. (2000). Quart. Rev. Biophys. 33: 371–424
Steinbach P.J., Brooks B.R. (1994). J. Comput. Chem. 15: 667–683
Stevensson B., Landersjö C., Widmalm G., Maliniak A. (2002). J. Am. Chem. Soc. 124: 5946–5947
Stevensson B., Sandström D., Maliniak A. (2003). J. Chem. Phys. 119: 2738–2746
Söderman P., Oscarson S., Widmalm G. (1998). Carbohydr. Res. 312: 233–237
Thaning, J., Stevensson, B. and Maliniak, A. (2005) J. Chem. Phys. 123, 044507-1-6
Thomas P.D., Basus V.J., James T.L. (1991). Proc. Natl. Acad. Sci. USA 88: 1237–1241
Tjandra, N. and Bax, A. (1997a) J. Magn. Reson. 124, 512–515
Tjandra, N. and Bax, A. (1997b) Science 278, 1111–1114
Tolman J.R., Al-Hashimi H.M., Kay L.E., Prestegard J.H. (2001). J. Am. Chem. Soc. 123: 1416–1424
van Buuren B.N.M., Schleucher J., Wittmann V., Griesinger C., Schwalbe H., Wijmenga S.S. (2004). Angew. Chem. Int. Ed. 43: 187–192
Wang C., Arthur G., Palmer A.G. III (2003). Magn. Reson. Chem. 41: 866–876
Widmalm G., Byrd R.A., Egan W. (1992). Carbohydr. Res. 229: 195–211
Acknowledgements
This work was supported by grants from the Carl Trygger Foundation, the Swedish Research Council, the Magnus Bergvall Foundation, and SIDA/SAREC. We thank the Center for Parallel Computers, KTH, Stockholm, for putting computer facilities at our disposal and Dr. Johan Weigelt for helpful discussions. Finally, we thank a reviewer for useful comments on the analysis of the experimental data.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Appendices
Appendix
APME procedure: a hybrid model based on maximum entropy and molecular field theory
The crucial step in the analysis of residual dipolar couplings (RDCs) in flexible molecules involves construction of the torsion angle distribution function for the molecular fragment under consideration. The RDC for a fixed conformational state Φ is given by
where the dipole–dipole coupling constant is defined as \(b_{ij}(\Phi)=-{\mu_0\gamma_i\gamma_j\hbar}/8\pi^2 r_{ij}^3 (\Phi)\) and D 2 n,m (Ω) is the second rank Wigner function (Brink and Satchler, 1993). Note that the averaging in Equ- ation A.1 refers only to molecular orientations. Thus, the order parameters 〈D 20,m (ΩDM)〉 become conformation dependent via the probability distribution function \(P(\beta, \gamma, \Phi)\). The transformation between the principal axis system (P) of the dipolar interaction and the laboratory frame (L) is performed explicitly using three successive rotations. Transformation between frame P and the molecular frame is characterized by ΩMP, whereas the Euler angles \(\beta, \gamma\) that specify relative orientations of molecular and director frames are denoted ΩDM. Finally, the orientation of the director in the magnetic field is given by ΩLD. The bicelles, in the present study, orient with the normal orthogonal to the field, which results in D 20,0 (ΩLD)=−1/2. Thus in the following we will consider this rotation as a constant factor and omit it in the equations.
The additive potential (AP) model. The AP model rests on equilibrium statistical mechanics and the mean potential \(U(\beta, \gamma, \Phi)\) is related to the singlet ODF by (Emsley et al., 1982)
where \(U(\beta, \gamma, \Phi)\), in units of RT, is written as the sum
The conformational potential U int (Φ) is independent of molecular orientation and it is usually expressed as a cosine series. The potential of mean torque, \(U_{\rm {ext}}(\beta, \gamma, \Phi)\), is written as
where the interaction parameters \(\upvarepsilon_{2,n} (\Phi)\) depend on the segmental, anisotropic interactions. The conformation dependence of these parameters is␣achieved by expressing them in terms of Φ-independent coefficients, \(\upvarepsilon_{2,p}^l\), which represent the interactions of the lth rigid subunit with the liquid crystalline field. Thus
where Ω lM is the orientation of the lth subunit in the molecular frame.
We will now consider a situation where the orientational order is low, which in turn implies that the potential of mean torque, \(U_{\rm {ext}}(\beta, \gamma, \Phi)\), is small. In this case, the ODF can be Taylor expanded and truncated after the second term. The analytical averaging over the molecular orientations, gives the distribution function corresponding to the low order limit of the AP model, P ′AP (Φ) (Stevensson et al., 2002, 2003; Thaning et al., 2005)
where P iso (Φ) is related to the internal potential U int(Φ), and Z′, Z′/4π are the normalization constants for P ′AP (Φ) and P iso(Φ), respectively. Thus, for a weakly ordered system, P ′AP (Φ)=P iso(Φ). The integral over the second term in Equation A.6 vanishes for all n due to properties of the Wigner functions (Brink and Satchler, 1993). Using the low order approximation and Equation A.4, we can express the conformation-dependent order parameters
The Kronecker delta δ n,m is a consequence of the orthogonality of the Wigner functions (Brink and Satchler, 1993), and Q(Φ)=4πexp{−U int(Φ)} is the conformation dependent partition function.
The R2R disaccharide consists of two rigid subunits R and R′, in which the coordinate frames are fixed with a relative orientation given by \(\Omega_{RR^{\prime}}\). The molecular coordinate frame (M) can be arbitrarily chosen to coincide with one of these rigid subunits. Using Equations A1, A5, and A7, we can define a conformation-dependent but orientationally averaged RDC
where the molecular frame was arbitrarily fixed in the subunit R′. Using the closure properties of the Wigner functions (Brink and Satchler, 1993), Equation A.8 can be simplified to
In Figure 2 we show the location of the various frames relevant for the analyses of the RDCs.
Combination of the AP and ME approaches: the APME model. Assuming low orientational order, the conformational distribution function P ′AP (Φ) was related, in Equation A.6, to the internal potential U int(Φ). The conformational distribution function for the glycosidic linkage in R2R depends on the torsion angles \(\upphi\) and \(\uppsi\). The choice of the functional form for the potential functions for these angles is not obvious. The least biased approach that requires minimum a priori information is the ME method (Catalano et al., 1991). We therefore use the ME approach to describe the conformational dependence of the RDCs. In addition, the functional form of the ME method facilitates inclusion of the conventional NMR parameters (NOEs and J-couplings) used in present study for structure determination. Combination of the low orientational order approximation of the AP model with the ME distribution function yields the APME distribution function (Stevensson et al., 2003) given in Equation 4.
Rights and permissions
About this article
Cite this article
Landersjö, C., Stevensson, B., Eklund, R. et al. Molecular conformations of a disaccharide investigated using NMR spectroscopy. J Biomol NMR 35, 89–101 (2006). https://doi.org/10.1007/s10858-006-9006-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10858-006-9006-0