Deformation under combined compression and shear: a new kinematic solution

Abstract

The conventional model of compression test, cylindrical profile model (CPM), ignores shearing deformation in the sample and yields an unrealistic solution. This article presents a new kinematic model and a closed-form solution for barrelled compression test. This model, exponential profile model (EPM), accounts for shear deformation in the test sample and provides a foundation to develop a detailed constitutive framework. To benchmark EPM, example solutions of the test are performed using a finite element model. The example results are compared with those of CPM. It is shown that CPM cannot evaluate the test’s real and non-uniform deformation. It is also shown that EPM’s predictions comply reasonably well with the finite element results. The importance of the presented solution can be better understood by noting that closed-form solutions of the mechanical tests are the most convenient routes to post process the raw test data and eventually to characterize the sample’s material. It is concluded that EPM is a far more reliable platform compared to CPM for meaningful interpretations of the test results.

Appendix

EPM’s axial velocity component, $\dot{v}$, is linked to its radial component, $\dot{u}$, via the incompressibility condition. To identify $\dot{v}$, one needs to calculate strain rate components that appear in the incompressibility condition, namely radial and tangential strain rate components in the cylindrical coordinate system, using Eq. 2:

$$ \dot{\varepsilon }_{rr} = \frac{{\partial \dot{u}}}{\partial r} = Az + B\dot{H} $$

(9)

$$ \dot{\varepsilon }_{\theta \theta } = \frac{{\dot{u}}}{r} + \frac{1}{r}\frac{{\partial \dot{w}}}{\partial \theta } = \frac{{\dot{u}}}{r} = Az + B\dot{H} $$

(10)

The axial strain rate component, $\dot{\varepsilon }_{zz}$, can be calculated as:

$$ \dot{\varepsilon }_{zz} = \frac{{\partial \dot{v}}}{\partial z} $$

(11)

Enforcing the incompressibility condition, by vanishing dilatometric summation $\dot{\varepsilon }_{zz} + \dot{\varepsilon }_{rr} + \dot{\varepsilon }_{\theta \theta } = 0$, results in the following partial differential equation:

$$ \frac{{\partial \dot{v}}}{\partial z} + 2\left( {Az + B\dot{H}} \right) = 0 $$

(12)

Solving Eq. 12, the specific solution is found as:

$$ \dot{v}\left( z \right) = - Az^{2} - 2B\dot{H}z + C_{1} $$

(13)

where $C_{1}$ is the constant of integral. To allow a zero axial velocity in the mid-plane, we employ $\dot{v}\left( 0 \right) = 0$ which results in $C_{1} = 0.$ The axial velocity becomes:

$$ \dot{v}\left( z \right) = - Az^{2} - 2B\dot{H}z $$

(14)

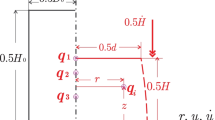
A boundary condition at the top sample–platen interface, $\dot{v}\left( {0.5H} \right) = - 0.5\dot{H},$ is used (Fig. 3c, d) to identify $A$:

$$ A = 2\frac{{\left( {1 - 2BH} \right)\dot{H}}}{{H^{2} }} $$

(15)

Substituting $A$ from Eq. 15 into Eqs. 2 and 14, $\dot{u}\left( {r,z} \right)$ and $\dot{v}\left( z \right)$ can be calculated as shown in Eqs. 3 and 4.

Equation 3 shows that $\dot{u}\left( {r,z} \right)$ is linear with respect to $r$ and $z$. Also, the axial velocity component, $\dot{v}\left( z \right)$, is a quadratic polynomial of $z$.

EPM’s strain rates in the sample

Using Eqs. 3 and 4, normal strain rate components (i.e. axial, radial and tangential) can be found as:

$$ \dot{\varepsilon }_{zz} = \frac{{\partial \dot{v}}}{\partial z} = - 2\dot{H}\frac{{\left( {BH\left( {H - 4z} \right) + 2z} \right)}}{{H^{2} }} $$

(16)

$$ \dot{\varepsilon }_{rr} = \frac{{\partial \dot{u}}}{\partial r} = \dot{H}\left( {B - \frac{{6\left( {1 + 2BH} \right)z^{2} }}{{H^{3} }}} \right) $$

(17)

$$ \dot{\varepsilon }_{\theta \theta } = \frac{{\dot{u}}}{r} = \dot{H}\left( {B - \frac{{6\left( {1 + 2BH} \right)z^{2} }}{{H^{3} }}} \right) $$

(18)

In addition, shearing components of strain rate in the sample can be found as:

$$ \dot{\varepsilon }_{rz} = \frac{1}{2}\left( {\frac{{\partial \dot{u}}}{\partial z} + \frac{{\partial \dot{v}}}{\partial r}} \right) = \dot{H} \frac{{\left( {1 - 2BH} \right)r}}{{H^{2} }} $$

(19)

$$ \dot{\varepsilon }_{r\theta } = \frac{1}{2}\left( {\frac{1}{r}\frac{{\partial \dot{u}}}{\partial \theta } + \frac{{\partial \dot{w}}}{\partial r} - \frac{{\dot{w}}}{r}} \right) = 0 $$

(20)

$$ \dot{\varepsilon }_{z\theta } = \frac{1}{2}\left( {\frac{{\partial \dot{w}}}{\partial z} + \frac{1}{r}\frac{{\partial \dot{v}}}{\partial \theta }} \right) = 0 $$

(21)

Real forming processes typically involve multi-axial strains including shearing deformation. Equation 19 estimates the only non-zero shearing component of deformation in the sample. When the test is used for physical simulation of a real process, the component plays a key role to produce a representative microstructure in the sample.

Assuming a von Mises material, effective plastic strain rate becomes:

$$ \dot{\bar{\varepsilon }} = \sqrt {\frac{2}{3}\dot{\varepsilon }_{ij} \cdot \dot{\varepsilon }_{ij} } = \sqrt {\frac{2}{3}\left( {\dot{\varepsilon }_{rr}^{2} + \dot{\varepsilon }_{\theta \theta }^{2} + \dot{\varepsilon }_{zz}^{2} + \frac{1}{2}\left( {\dot{\gamma }_{rz}^{2} + \dot{\gamma }_{z\theta }^{2} + \dot{\gamma }_{r\theta }^{2} } \right)} \right)} $$

(22)

Vanishing the zero components and noting $\varepsilon_{rr} = \varepsilon_{\theta \theta } = - \frac{1}{2}\varepsilon_{zz}$, Eq. 22 simplifies as:

$$ \dot{\bar{\varepsilon }} = \sqrt {\frac{2}{3}\left( {6 \dot{\varepsilon }_{rr}^{2} + 2\dot{\varepsilon }_{rz}^{2} } \right)} $$

(23)

Substituting the terms in Eq. 23 and simplifying, EPM’s effective strain rate becomes as shown in Eq. 5.

EPM’s effective strain calculations

The strain components can be found after integrating their corresponding strain rate components along the deformation streamlines. These will be carried out next using ${\text{d}}t = \frac{{ - {\text{d}}H}}{{\dot{H}}}$ to change the integration variable. After simplifying integrations, the results become:

$$ \varepsilon_{rr} = \frac{ - 1}{{\dot{H}}}\mathop \smallint \limits_{{H_{0} }}^{H} \dot{\varepsilon }_{rr} {\text{d}}H = \frac{{\left( {H_{0} - H} \right)\left( {BH_{0} H + 2z} \right)}}{{H_{0} H}} + 4Bz\left( {\ln H - \ln H_{0} } \right) $$

(24)

$$ \varepsilon_{\theta \theta } = \frac{ - 1}{{\dot{H}}}\mathop \smallint \limits_{{H_{0} }}^{H} \dot{\varepsilon }_{\theta \theta } {\text{d}}H = \frac{{\left( {H_{0} - H} \right)\left( {BH_{0} H + 2z} \right)}}{{H_{0} H}} + 4Bz\left( {\ln H - \ln H_{0} } \right) $$

(25)

$$ \varepsilon_{zz} = \frac{ - 1}{{\dot{H}}}\mathop \smallint \limits_{{H_{0} }}^{H} \dot{\varepsilon }_{zz} {\text{d}}H = \frac{{2\left( {H - H_{0} } \right)\left( {BHH_{0} + 2z} \right)}}{{HH_{0} }} + 8Bz\left( {\ln H_{0} - \ln H} \right) $$

(26)

$$ \varepsilon_{rz} = \frac{ - 1}{{\dot{H}}}\mathop \smallint \limits_{{H_{0} }}^{H} \dot{\varepsilon }_{rz} {\text{d}}H = r\left( {\frac{{H_{0} - H}}{{HH_{0} }} + 2B\left( {\ln H - \ln H_{0} } \right) } \right) $$

(27)

the effective strain is defined as:

$$ \bar{\varepsilon } = \sqrt {\frac{2}{3}\left( {\varepsilon_{rr}^{2} + \varepsilon_{\theta \theta }^{2} + \varepsilon_{zz}^{2} + 2\varepsilon_{rz}^{2} } \right)} $$

(28)

Substituting terms in Eq. 28 and simplifying, EPM’s effective strain becomes as shown in Eq. 6.

CPM’s strain rates and strains

A brief description of the conventional cylindrical profile model is presented here to facilitate its comparison with the proposed model, EPM.

In the conventional cylindrical profile model, the following simple kinematic descriptions are used:

$$ \dot{u}'\left( r \right) = \frac{{\dot{D}r}}{D} = - \frac{{r\dot{H}}}{2H},\quad \dot{v}^{'} \left( z \right) = \frac{{z\dot{H}}}{H},\quad \dot{w} = 0 $$

(29)

Using definitions of strain rate components for the conventional model in the cylindrical coordinate system:

$$ \dot{\varepsilon }_{rr} = \dot{\varepsilon }_{\theta \theta } = - \frac{1}{2}\dot{\varepsilon }_{zz} = - \frac{{\dot{H}}}{2H} $$

(30)

also $\dot{\varepsilon }_{y\theta } = \dot{\varepsilon }_{r\theta } = \dot{\varepsilon }_{yr} = 0$ and it can be shown that the resulting normal strain components satisfy the compressibility equation. Also, the equivalent strain rate becomes:

$$ \dot{\bar{\varepsilon }} = \sqrt {\frac{2}{3}} \left( {\dot{\varepsilon }_{rr}^{2} + \dot{\varepsilon }_{zz}^{2} + \dot{\varepsilon }_{\theta \theta }^{2} } \right)^{0.5} = \frac{{\dot{H}}}{H} $$

(31)

The effective strain for this model can be estimated as:

$$ \bar{\varepsilon } = \frac{ - 1}{{\dot{H}}}\mathop \smallint \limits_{{H_{0} }}^{H} \dot{\bar{\varepsilon }}{\text{d}}H = - 1\mathop \smallint \limits_{{H_{0} }}^{H} \frac{{{\text{d}}H}}{H} = \ln H_{0} - \ln H $$

(32)

Estimation of B

A prerequisite to find strain and strain rate in the sample is the barrelling parameter, $B.$ Details on definitions and computations of a barrelling parameter for EPM can be found elsewhere [25]. Here, the final expression required to calculate $B$ is presented for convenience.

The proposed EPM relies on the deformed geometrical parameters: $H$, $D$, $d$, $H_{0}$, $D_{0}$ and $B$. Given the parameters for a deformed geometry, EPM’s barrelling parameter $B$ can be estimated. We note that $d$ is a geometrical parameter that is relatively difficult to measure. The authors developed a technique to estimate $d$ based on the volume constancy principle and measured values of $H$, $D$, $H_{0}$ and $D_{0}$ [25].

Derivations of barrelling parameter $B$ are lengthy and complex. In fact, a full manuscript has been dedicated to the derivations [24]. This is partly due to the fact that there are several paths to estimate $B$. A simple estimate of the barrelling parameter, $B$, at its top interface with platen was provided in [24] as:

$$ B = \frac{{0.5\left( {H + H_{0} \ln \frac{d}{{D_{0} e}}} \right)}}{{0.5H_{0}^{2} - 0.5HH_{0} - HH_{0} \left( {\ln H_{0} - \ln H} \right)}} $$

(33)

Alternatively, barrelling parameter can be identified at the mid-plane; $z = 0$ and 2 $R = D_{n}$ to find $B$ as following [24]:

$$ B = \frac{{D_{n} - D_{n - 1} }}{{D_{n - 1} H_{n - 1} - D_{n - 1} H_{n} }} $$

(34)

where $n$ is the current deformation time step. Subscripts $n$ and $n - 1$ in Eq. 34 indicate that their associated parameters were measured at time steps of $n$ and $n - 1$, respectively. See Ref. [24] for details of the available routes to find $B$ using an incremental approach.