Amplitude and Frequency Variation in Nonlinear Glucose Dynamics with Multiple Delays via Periodic Perturbation

Abstract

Characterising the glycemic response to a glucose stimulus is an essential tool for detecting deficiencies in humans such as diabetes. In the presence of a constant glucose infusion in healthy individuals, it is known that this control leads to slow oscillations as a result of feedback mechanisms at the organ and tissue level. In this paper, we provide a novel quantitative description of the dependence of this oscillatory response on the physiological functions. This is achieved through the study of a model of the ultradian oscillations in glucose-insulin regulation which takes the form of a nonlinear system of equations with two discrete delays. While studying the behaviour of solutions in such systems can be mathematically challenging due to their nonlinear structure and non-local nature, a particular attention is given to the periodic solutions of the model. These arise from a Hopf bifurcation which is induced by an external glucose stimulus and the joint contributions of delays in pancreatic insulin release and hepatic glycogenesis. The effect of each physiological subsystem on the amplitude and period of the oscillations is exhibited by performing a perturbative analysis of its periodic solutions. It is shown that assuming the commensurateness of delays enables the Hopf bifurcation curve to be characterised by studying roots of linear combinations of Chebyshev polynomials. The resulting expressions provide an invaluable tool for studying the interplay between physiological functions and delays in producing an oscillatory regime, as well as relevant information for glycemic control strategies.

1 Introduction

Homoeostasis refers to the body’s ability to maintain certain variables within a narrow range and is a result of the negative feedback loops which occur within the body (Cannon 1932; Thomas et al. 1995). These loops keep the parameters involved at, or close to, a healthy value, or steady state (Thomas et al. 1995). The steady state may be stable, leading to constant levels over time, or unstable, leading to sustained oscillations (Thomas et al. 1995). Examples of homoeostatic processes include: the regulation of temperature; blood pressure; glucose concentration; percentage of water within the cells; and calcium levels. While many biological systems can be modelled with ordinary differential equations (ODEs), delays can so often prove crucial in realistically replicating core aspects of these systems (Thomas et al. 1995). Indeed, a lot of work has gone into determining the role of these delayed recurrent loops in physiology (Bocharov and Rihan 2000), especially in hormonal systems (Walker et al. 2012, 2010). For example, in the case of modelling the glucose–insulin regulatory system, an ODE system with subsystems replicating delay can replicate the ultradian rhythms that occur naturally in the system without the need for postulating an internal pulsatile insulin pacemaker (Levy 2001; Sturis et al. 1991).

This paper focuses on the ultradian rhythms that occur within the glucose–insulin system. As discussed in O’Meara et al. (1993), insulin resistance has been observed to gradually dampen the oscillations, culminating in a loss of synchronisation between glucose and insulin. While insulin resistance may be present in patients without diabetes, it is generally associated with patients with type 2 diabetes (T2DM), and so we take the accurate tuning of the ultradian oscillations to be a sign of healthy regulation (Huard et al. 2017). We then propose the following question:

What is the effect of diabetic parameters on the amplitude and period of the ultradian rhythms?

To answer this question, we introduce a perturbative scheme for the periodic solutions of a two-compartment delay differential equation (DDE) model of the ultradian rhythms in the glucose–insulin regulatory system based on the Poincaré–Lindstedt (P–L) method. The model is a polynomial expansion of the system presented in Huard et al. (2017), which was originally created in Sturis et al. (1991). A large number of authors developed and studied this model to characterise its local and global stability properties and characterise its periodic solutions (Bennett and Gourley 2004; Engelborghs et al. 2001; Giang et al. 2008; Huard et al. 2015; Kissler et al. 2014; Li and Kuang 2007; Li et al. 2006; Wang et al. 2009). As far as we are aware, this is the first time that the P–L method has been applied to a model of glucose and insulin regulation. It has been applied to other biological systems such as in Verdugo and Rand (2008), where it was used to predict the amplitude and frequency for a two-compartment DDE model of gene expression with one delay. Similarly, in Brandt et al. (2006), the frequency of a two-compartment DDE model for describing two couple Hopfield neurons was calculated. To the best of our knowledge, in all cases where this technique has been applied to dynamical systems with n components and multiple delays $\tau _i$’s, the characteristic equation defining the eigenmodes $\lambda$’s is an exponential polynomial of the form

$$\begin{aligned} c_n \lambda ^n + c_{n-1} \lambda ^{n-1} + \cdots + c_0 + e^{-\lambda \sum _i \tau _i} = 0, \quad c_i \in \mathbb {R}, \quad \tau _i \in \mathbb {R}^{+}, \quad \lambda \in \mathbb {C}, \end{aligned}$$

(1)

in which the polynomial part is typically Hurwitz stable. Thus, for these systems, delays interact in a linear manner to give rise to a supercritical Hopf bifurcation at a point in the space of delays which can be obtained, along with the characteristic frequency, by using imaginary root crossing methods (Cooke and Van Den Driessche 1986; Kuang 1993).

The system studied in this paper, which is presented in Sect. 2, contains two delays, $\tau _1$ and $\tau _2$, and poses the additional challenge that the characteristic equation involves two exponentials. Although crossing curves can be described in this situation using geometric arguments (Gu et al. 2005), we show that characteristic frequencies can be obtained by studying the zeroes of linear combinations of Chebyshev polynomials of the first type. This is achieved by assuming the commensurateness of delays, that is, $\tau _2 = \kappa \tau _1$, where $\kappa \in \mathbb {Z^+}$ is a coupling parameter. This assumption does not lead to additional restrictions and allows us to define a group of lines in the space of delays along which the perturbative scheme can be defined. Furthermore, it enables the study of solutions for physiologically relevant ranges of the model parameters.

In summary, the paper aims to provide a way of quantifying the contribution of model parameters to the amplitude and period of the ultradian rhythms in the glucose–insulin regulatory system. An analysis of the effect of each physiological feature on the limit cycles, with a particular focus on insulin resistance, is then described. The work is divided as follows. After presenting the model in Sect. 2, local stability properties and conditions for the boundedness of trajectories are detailed in Sect. 3. In Sect. 4, the P–L method is applied in order to obtain approximate formulas for the amplitude and period of the oscillations. Section 5 is dedicated to the study of the influence of model parameters on the oscillations. Finally, physiological implications are explored, along with concluding outlooks.

2 Model

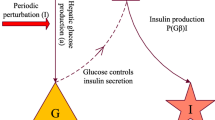
The model under consideration follows the framework given in Fig. 1 and is a two-compartment first-order polynomial DDE system given by

$$\begin{aligned} \dot{G}(t)&= a_0 - a_1 G(t) - a_2 G(t) I(t) - a_3 I(t - \tau _2)^p, \nonumber \\ \dot{I}(t)&= b_1 G(t-\tau _1)^n - b_2 I(t), \quad n\in 2\mathbb {Z}, \quad p \in \mathbb {Z}^{+}, \end{aligned}$$

(2)

where G(t) is the plasma glucose concentration (in mg) and I(t) is the plasma insulin concentration (in mU). By noting that, within the plasma, the volume of glucose space is around 100dl while that of insulin distribution is approximately 3l (Sturis et al. 1991), G(t) and I(t) are converted to concentrations (mg/dl and mU/l, respectively), for the purpose of all figures. All parameters are assumed to be nonzero and have units as defined in Table 1.

Fig. 1

Flow diagram for model (2)

The coefficients $a_1$ and $a_2$ describe the insulin independent and dependent glucose utilisations respectively. The parameter $a_0 = G_{in} + C$ includes two contributions, namely $G_{in}$ which corresponds to a constant glucose infusion, and the constant C which partially represents the hepatic glucose production. Indeed, following the work of Huard et al. (2015), Li et al. (2006) and Sturis et al. (1991), we note that hepatic glucose production can be represented by a rational function of the type

$$\begin{aligned} \text {Hepatic} \approx \frac{K_0}{K_1+I(t-\tau _2)^p} \approx C - a_3 I(t - \tau _2)^p, \end{aligned}$$

where $\tau _2$ corresponds to the time taken for variations in insulin levels to have an observable effect on hepatic glucose production, in minutes. In the insulin balance equation, $b_1$ is the insulin production capability of the individual, and $b_2$ is the insulin degradation rate. While the insulin secretion term appears to be unbounded, we note that it is usually modelled using a sigmoidal function (Huard et al. 2015; Li et al. 2006; Sturis et al. 1991),

$$\begin{aligned} \text {Pancreatic} \approx \frac{G(t - \tau _1)^n}{G(t - \tau _1)^n + K_2} \approx \frac{G(t - \tau _1)^n}{K_2^n} = b_1 G(t - \tau _1)^n, \end{aligned}$$

where $\tau _1$ is the time taken for insulin to be secreted and transported to the interstitial space in response to elevated glucose levels. Hence, the secretion function is a local approximation of a bounded function. Thus, although the polynomial form of the system contrasts with previous models in which the hepatic and pancreatic secretions are represented by bounded sigmoidal functions (Bennett and Gourley 2004; Huard et al. 2015; Li et al. 2006), it is appropriate for studying dynamics in the neighbourhood of the limit cycle. To further aid in the study of the model dynamics, we shall later take the delay $\tau _2$ to be commensurate with $\tau _1$. It is worth noting that the convergence speed to this limit cycle may be altered through this approximation. Boundedness and positivity of trajectories can also be affected through the polynomial approximation, as investigated in Sect. 3.2.1.

Table 1 Units for the parameters in model (2)

3 Local Stability Analysis

The presence of Hopf bifurcations in model (2) strongly depends on the values of delays. We divide our analysis into two parts. Firstly, we investigate conditions for the one-delay model (with $a_3 = 0$) to undergo a Hopf bifurcation. Secondly, the bifurcation curve in the two-delay model is investigated by assuming commensurateness of delays.

3.1 Constant Hepatic Glucose Production

Here, we look to find conditions on parameter values in the polynomial model (2) with $a_3 = 0$ ensuring the presence of oscillations in an appropriate range. Equivalently, this amounts to investigating the second-order approximation of (2) when $p>2$. In this case, only the constant term from hepatic production remains, namely

$$\begin{aligned} \dot{G}(t)&= G_{in} - a_1 G(t) - a_2 G(t) I(t) + C,\nonumber \\ \dot{I}(t)&= b_1 G(t-\tau )^n - b_2 I(t), \quad \tau = \tau _1. \end{aligned}$$

(3)

Although $\tau _2$ does not appear in the resulting system, the minimal model (3) captures the role of the delay $\tau _1$ in producing an oscillatory regime. Incidentally, it was observed numerically that the contribution of $\tau _1$ to the amplitude and period of the oscillations is more prominent than that of $\tau _2$ (Li et al. 2006). Furthermore, the positivity and boundedness of trajectories for system (3) is easily demonstrated following the arguments formulated in Bennett and Gourley (2004) and Shi et al. (2017).

3.1.1 Value of Parameters

Given an oscillatory solution, the inverse problem of choosing parameters in model (3) can be addressed in the following way. We note that the system’s steady state ($\bar{G}$, $\bar{I}$) satisfies the equations

$$\begin{aligned} \bar{I}= \frac{b_1 {\bar{G}}^n}{b_2}, \quad a_2 b_1 \left( \bar{G}\right) ^{n+1} + \left( a_1 b_2\right) \bar{G}- a_0 b_2 = 0. \end{aligned}$$

(4)

By Descartes’ rule of signs, (4) has exactly one positive root for $\bar{G}$, and so one can always find a positive $(\bar{G},\bar{I})$. Here we assume that the target basal levels can be identified with the steady state of the system.

• 1. It has been shown that the insulin clearance is proportional to the plasma insulin concentration (Koschorreck and Gilles 2008; Topp et al. 2000). Numerical fitting procedures have rendered values for $b_2$ in the range (0.03, 0.3) (Chen et al. 2010). As in Huard et al. (2017), Huard et al. (2015) and Li et al. (2006), we shall choose an initial value of $b_2 = 0.06$ for most numerical computations with the reduced model. The value of $b_1$ is then obtained as $b_1 = b_2 \bar{I}\bar{G}^{-n}$.

• 2. The system must be in an oscillatory state. Therefore, the delay $\tau \in \mathbb {R}^{+}$ must be larger than the critical value $\tau _{0}$ such that the characteristic equation

  $$\begin{aligned} (\lambda + b_2)(\lambda + a_1 + a_2 \bar{I}) + n a_2 b_2 \bar{I}e^{-\lambda \tau _0}=0, \quad \lambda \in \mathbb {C}, \end{aligned}$$

  (5)

  possesses a set of conjugate purely imaginary root $\lambda = \pm i \omega _0$. This requirement implies that the critical pair ($\omega _0, \tau _{0})$ satisfies the system

  $$\begin{aligned} n a_2 b_2 \bar{I}\cos {(\omega _0 \tau _{0})} = \omega _0^2 - b_2 (a_1 + a_2 \bar{I}), \quad n a_2 b_2 \bar{I}\sin {(\omega _0 \tau _{0})} = (b_2 + a_1 a_2 \bar{I}) \omega _0. \end{aligned}$$

  (6)

  This in turns implies that $\omega _0$ satisfies a quartic equation

  $$\begin{aligned} \omega _0^4+ \omega _0 ^2 \left( (a_1 + a_2 \bar{I})^2 +b_2^2 \right) +b_2^2 \left( \left( a_1 + a_2 \bar{I}\right) ^2 - \left( n a_2 \bar{I}\right) ^2 \right) =0. \end{aligned}$$

  (7)

  Requiring that Eq. (7) possesses a positive root for $\omega _0$ gives explicit conditions on the coefficients for the existence of a Hopf bifurcation. Since the middle term in (7) is always positive, one must have $n> \frac{a_1}{a_2 \bar{I}} + 1 > 1,$ in order to have a bifurcation. Consequently, the periodic perturbation scheme presented in Sect. 4.1 shall focus on the case $n=2$, which implies that $a_1 < a_2 \bar{I}$. The value of $\tau _0$ is then obtained from (6) as

  $$\begin{aligned} \tau _0 = \frac{1}{\omega _0} \left( \mathrm {arccos}\left( \frac{\omega _0^2 - b_2(a_1 + a_2 \bar{I})}{2 a_2 b_1 \bar{G}^2}\right) + 2 K \pi \right) , \end{aligned}$$

  (8)

  where $K \in \mathbb {Z}^+$ is the smallest integer such that (8) defines a positive value. Larger values of K give successive $\tau _0$ values for which stability switches may occur in the linear system. However, for the nonlinear system (3), it is numerically observed that oscillations are present whenever $\tau \ge \tau _0$.

• 3. The constant $a_0 = G_{in} + C$ is then obtained from the steady-state equation, $a_0 = a_1 \bar{G}+ a_2 \bar{G}\bar{I}.$ The parameters $a_1$ and $a_2$ must be chosen such that oscillations are present for a physiologically relevant value of the critical delay $\tau _0$. For different values of $b_2$, one can numerically compute the range of achievable values for $\tau _0$ using Eq. (8) (see Figure 9 in Bridgewater et al. 2019).

This approach provides a model able to replicate the nonlinear oscillations within an appropriate physiological range (Fig. 2).

Fig. 2

Oscillations described by the minimal model (3) using the following parameter values: $a_0 = 1300, a_1 = 2.03 \times 10^{-4}, a_2 = 0.0017, b_1 = 6.01 \times 10^{-8}, b_2 = 0.06, \tau =20$

3.2 Extension to Two Delays

We now consider the problem of studying periodic solutions in the two-delay system (2). In the first instance, we investigate the question of boundedness and positivity of trajectories of the system. In the second, the characterisation of periodic solutions in the two-dimensional space of delays is achieved by assuming the commensurateness of delays, i.e. $\tau _2 = \kappa \tau _1$, with $\kappa \in \mathbb {Z}^+$.

3.2.1 Positivity and Boundedness

Here we look for conditions for the positivity and boundedness of solutions in the polynomial initial value problem

$$\begin{aligned} \dot{G}= & {} a_0 - a_1 G - a_2 G I - a_3 I(t-\tau _2)^p, \quad \dot{I} = b_1 G(t-\tau _1)^n - b_2 I,\nonumber \\ G(t)= & {} \varphi (t), \quad I(t) = \phi (t), \quad t \in [-\max {(\tau _1,\tau _2)},0], \end{aligned}$$

(9)

where $\phi , \varphi$ are continuous strictly positive functions on $[-\max {(\tau _1,\tau _2)},0]$, $p \in \mathbb {Z}^+$ and n is a strictly positive even integer, which is the typical case in insulin secretion modelling studies (e.g. Topp et al. 2000; Yang et al. 2016).

As mentioned previously, positivity and boundedness of solutions for model (9) when $a_3 = 0$ can be established using the same techniques as in Bennett and Gourley (2004) and Shi et al. (2017). Here, the additional non-positive and possibly nonlinear term when $a_3 \ne 0$ can lead to unbounded trajectories and to the development of singularities in finite time. Nonetheless, the positivity of I(t) can be easily established.

Proposition 1

For all solutions of (9) and $\forall t>0$, we have that $I(t)>0$. Furthermore, $\forall t>\tau _2$, the following inequality can be established

$$\begin{aligned} I(t) \ge e^{-b_2 \tau _2} I(t-\tau _2). \end{aligned}$$

Proof

Indeed, from the second equation in (9), we have

$$\begin{aligned} I(t) = e^{-b_2 t} \left[ b_1 \int _0^t G(s-\tau _1)^n e^{b_2 s} ds + I(0) \right] , \end{aligned}$$

(10)

which implies the positivity of I(t) since n is assumed to be a positive even integer. Equation (10) also leads to

$$\begin{aligned} I(t-\tau _2)= & {} e^{-b_2 (t-\tau _2)} \left[ b_1 \int _0^{t-\tau _2} G(s-\tau _1)^n e^{b_2 s} ds + I(0) \right] \nonumber \\\le & {} e^{b_2 \tau _2} e^{-b_2 t} \left[ b_1 \int _0^{t} G(s-\tau _1)^n e^{b_2 s} ds + I(0)\right] = e^{b_2\tau _2} I(t). \end{aligned}$$

(11)

$\square$

Due to the biological nature of the problem, unbounded solutions are not in the scope for applications, and therefore, we shall focus on parameter values not leading to such solutions. The following holds true.

Proposition 2

If G(t) is strictly positive $\forall t>0$, then G(t) and I(t) are bounded from above.

Proof

Let G(t) be positive for all times $t>0$. Then, since $I(t) >0$, we have that $\dot{G} \le a_0 - a_1 G,$ and therefore $G(t) \le G_{+} = \mathrm {min}\left\{ G(0),\frac{a_0}{a_1}\right\} < \infty$. In turn, we obtain that $\dot{I} \le b_1 G_{+}^n - b_2 I,$ giving $I(t) \le I_{+} = \mathrm {min}\left\{ I(0), \frac{b_1 G_{+}^n}{b_2}\right\} < \infty$.$\square$

The converse can be established in the following case.

Corollary 1

Let I(t) be bounded from above, $0 \le I(t) \le I_{+} < \infty$, with $a_0 > a_3 I_{+}^p$. Then G(t) is positive and bounded for all $t>0$ if $G(0) >0$.

Proof

From the first equation in system (12), it can be easily seen that

$$\begin{aligned} G(t) = e^{ - \int _0^t (a_1 + a_2 I(s)) \, ds} \left( G(0) + \int _0^t (a_0 - a_3 I(s-\tau _2)^p) e^{\int _0^s (a_1+a_2 I(u)) \, du} \, ds\right) , \end{aligned}$$

Hence G(t) is strictly positive for all t if $a_0 > a_3 I_{+}^p$ and $G(0) >0$, and is therefore bounded by Proposition 2.$\square$

It is noteworthy to highlight that depending on the values taken for n and p, some solutions may become unbounded in finite time. A subclass of such blow-up solutions is represented by trajectories possessing poles for which the location depends on initial conditions. Such singularities, called movable poles, can be detected in the delay-free system using a local analysis of the Painlevé type (see e.g. Conte 2012; Goriely and Hyde 1998, 2000). As shown in Appendix 1, the values $n=p=2$ may lead to this kind of singular solution. Consequently, the periodic perturbation scheme presented in Sect. 4.2 shall focus on the case $n=2, p=1$ to avoid unbounded solutions.

3.3 Periodic Solutions in System with Commensurate Delays

We now consider the problem of characterising periodic solutions in system (2) where delays are assumed to be commensurate, i.e. $\tau _2 = \kappa \tau _1$, with $\kappa \in \mathbb {Z}^+$. A straightforward generalisation can be made for the case when the delays are rationally related. This assumption allows to perform a perturbative analysis of the periodic solutions along the line $\tau _2 = \kappa \tau _1$, given that the point $(\tau _1, \kappa \tau _1)$ remains sufficiently close to the curve of Hopf bifurcations in the delay space $(\tau _1,\tau _2)$. Geometrically, this approach provides a discrete set of critical points, corresponding to the intersection between lines and the threshold curve (Fig. 3). We show that these crossing points can be described by studying the zeros of linear combinations of Chebyshev polynomials of the first kind.

Fig. 3

Threshold curve in the delay space with sections $\tau _2 = \kappa \tau _1$, $\kappa \in \mathbb {Z}^+$ defining the fan of expansion lines

In its most general form, model (2) with commensurate delays becomes

$$\begin{aligned} \dot{G} = a_0 - a_1 G - a_2 G I - a_3 I(t-\kappa \tau )^p, \quad \dot{I} = b_1 G(t-\tau )^n - b_2 y. \end{aligned}$$

(12)

Any equilibrium $(\bar{G}, \bar{I})$ of (12) obeys the equations

$$\begin{aligned} a_2 b_1 b_2^p \bar{G}^{1+n} + a_3 b_1^p b_2 \bar{G}^{n p} + a_1 b_2^{1+p} \bar{G}- a_0 b_2^{1+p} = 0, \quad \bar{I}= \frac{b_1}{b_2} \bar{G}^n, \end{aligned}$$

(13)

which always possess a unique strictly positive root since $a_i, b_i > 0$ and $n,p\in \mathbb {Z}^+$. The linearisation about this steady state ($\bar{G}, \bar{I}$) reads as

$$\begin{aligned} \left( \begin{array}{c} \dot{x} \\ \dot{y} \end{array}\right)&= \left( \begin{array}{ll} -(a_1 + a_2 \bar{I}) &{}\quad -a_2 \bar{G}\\ 0 &{}\quad -b_2 \end{array}\right) \left( \begin{array}{c} x \\ y \end{array}\right) + \left( \begin{array}{ll} 0 &{}\quad 0 \\ n b_1 \bar{G}^{n-1} &{}\quad 0 \end{array}\right) \left( \begin{array}{c} x_{\tau } \\ y_{\tau } \end{array}\right) \nonumber \\&\qquad + \left( \begin{array}{ll} 0 &{}\quad -a_3 p \bar{I}^{p-1} \\ 0 &{}\quad 0 \end{array}\right) \left( \begin{array}{c} x_{\kappa \tau } \\ y_{\kappa \tau } \end{array}\right) , \end{aligned}$$

(14)

where $x_{\tau } = x(t-\tau ), x_{\kappa \tau } = x(t-\kappa \tau )$ and similarly for y. The characteristic equation of (14) is a quasi-polynomial of the form

$$\begin{aligned} \lambda ^2 + A_1 \lambda + A_2 + A_3 e^{-\lambda \tau } + A_4 e^{-(\kappa +1) \lambda \tau } = 0, \quad \lambda \in \mathbb {C}, \quad \kappa \in \mathbb {Z^+}, \end{aligned}$$

(15)

where $A_1 = a_1 + a_2 \bar{I} + b_2, A_2 = b_2(a_1 + a_2 \bar{I}), A_3 = n a_2 b_1 \bar{G}^n, A_4 = n a_3 b_1 p \bar{G}^{n-1}\bar{I}^{p-1}$. Since $A_1, A_2, A_3, A_4 >0$, Eq. (15) is Hurwitz stable for $\tau = 0$ and we now look for conditions on $\kappa$ and $\tau$ ensuring that it undergoes a Hopf bifurcation. Hence, setting $\lambda = i \omega _0$, $\omega _0 >0$ leads to the system

$$\begin{aligned} \omega _0^2&= A_2 + A_3 \cos (\omega _0 \tau ) + A_4 \cos ((1+\kappa ) \omega _0 \tau ),\end{aligned}$$

(16)

$$\begin{aligned} A_1 \omega _0&= A_3 \sin (\omega _0 \tau ) + A_4 \sin ((1+\kappa ) \omega _0 \tau ). \end{aligned}$$

(17)

Eliminating polynomial occurrences of $\omega _0$, one is led to the following trigonometric equation

$$\begin{aligned}&A_1^2 (A_2 + A_3 \cos {(\omega _0 \tau )} + A_4 \cos ((1+\kappa ) \omega _0 \tau )) \nonumber \\&\quad = (A_3 \sin (\omega _0 \tau ) + A_4 \sin ((1+\kappa ) \omega _0 \tau ))^2. \end{aligned}$$

(18)

Setting $z = \cos {(\omega _0 \tau )}$, i.e. $\omega _0 \tau = \arccos {z}$, then $\cos {(n \omega _0 \tau )} = T_n(z)$, $\sin {(n \omega _0 \tau )} = \sqrt{1-z^2} U_{n-1}(z)$, where $T_n$ and $U_{n-1}$ are Chebyshev polynomials of the first and second kinds, respectively. Equation (18) implies that z satisfies the following polynomial equation

$$\begin{aligned} A_1^2 (A_2 + A_3 z + A_4 T_{1+\kappa }(z)) = (1-z^2) (A_3 + A_4 U_{\kappa }(z))^2. \end{aligned}$$

(19)

Further using the following well-known identities, for $n\ge m$,

$$\begin{aligned}&(1-z^2) U_{n-1}(z) = z T_n(z) - T_{n+1}(z), \\&2 (1-z^2) U_{n-1}(z) U_{m-1}(z) = T_{n-m}(z) - T_{n+m}(z), \end{aligned}$$

we obtain that (19) can be rewritten as a linear combination of Chebyshev polynomials of the first type

$$\begin{aligned}&A_4^2 T_{2 \kappa +2}(z) +2 A_3 A_4 T_{\kappa +2}(z) +2 A_1^2 A_4 T_{\kappa +1}(z) - 2 A_3 A_4 T_{\kappa }(z) \nonumber \\&\quad + A_3^2 T_2(z) + 2 A_1^2 A_3 T_1(z) + 2 A_1^2 A_2 - (A_3^2+A_4^2) = 0. \end{aligned}$$

(20)

For a given $\kappa \in \mathbb {Z}^+$, any real root of (20) with $|z|<1$ which gives a nonzero solution for $\omega _0$ through equations (16) and (17), which can be rewritten in terms of z as

$$\begin{aligned} \omega _0^2= & {} A_2 + A_3 z + A_4 T_{1+\kappa }(z), \end{aligned}$$

(21)

$$\begin{aligned} A_1 \omega _0= & {} \sqrt{1-z^2} (A_3 + A_4 U_{\kappa }(z)), \end{aligned}$$

(22)

leads to a non-constant periodic solution.

Example 1

Let us consider, for illustration, the special case $A_1=\cdots =A_4=\kappa =1$. Equation (20) reduces to

$$\begin{aligned} 2(1+2z)(2z^3+z^2-z-1) = 0. \end{aligned}$$

It is easily seen that the root $z = -1/2$ is the unique value leading to a null frequency ($\omega _0=0$), since $U_1(z)$ is linear. The presence of an additional root in the interval $(-1,1)$ can be assessed using, for instance, Sturm sequences (see, e.g. Bochnak et al. 2013). For the polynomial $2z^3+z^2-z-1$, the Sturm chain H(z) is given by

$$\begin{aligned} H(z) = \left\{ 2 z^3+z^2-z-1,6 z^2+2z-1,\frac{7z}{9}+\frac{17}{18},-\frac{31}{98} \right\} , \end{aligned}$$

which, when evaluated at the end points, gives

$$\begin{aligned} \mathrm {\# \text {sign changes}}(H(-1)) - \mathrm {\# \text {sign changes}}(H(1))=1. \end{aligned}$$

The corresponding unique positive root $z_0$ leads to the following explicit expressions for the critical pair $(\omega _0,\tau _0)$

$$\begin{aligned} \omega _0&=\frac{1}{3} \left( 2+\sigma _{-}+\sigma _{+}\right) \sqrt{1-\frac{1}{36} \left( \sigma _{-} + \sigma _{+}-1\right) ^2} \approx 1.485, \end{aligned}$$

(23)

$$\begin{aligned} \tau _0&= \frac{1}{\omega _0} \left[ \cos ^{-1}\left( \frac{1}{6} \left( \sigma _{-} + \sigma _{+} - 1\right) \right) + 2 m \pi \right] \approx 0.399 + \frac{2 m \pi }{\omega _0}, \end{aligned}$$

(24)

where $m=\mathbb {Z}^+$ and $\sigma _{\pm } = \root 3 \of {44 \pm 3 \sqrt{177}}$.

4 Hopf Bifurcation Formulae

We now turn to the main objective of this work, namely the analysis of the variation of amplitude and frequency in the nonlinear model with respect to the model parameters. This is achieved through the perturbation of periodic solutions in the linear model in a neighbourhood of the critical manifold. This technique is usually referred to as the P–L expansion and was extended to differential equations with explicit delay in Casal and Freedman (1980) and applied to a limited number of delayed models to highlight the contribution of parameters to the amplitude of oscillations (Brandt et al. 2006; Casal and Freedman 1980; Rand and Verdugo 2007; Verdugo and Rand 2008).

We first consider the case when hepatic glucose production is assumed to be constant (see model (25)), in which case the small bifurcation parameter $\epsilon >0$ represents the distance from the critical $\tau _0$. Secondly, we extend our considerations to the two delay case by assuming that the second delay is a constant multiple of the first one, thus defining a fan of expansion lines in the space of delays (see model (39)). Throughout this section, it is assumed that the frequency $\omega _0$ of the periodic solution of the linearised system does not satisfy an equation of order lower than the characteristic equation.

4.1 Constant Hepatic Glucose Production

Recall from Sect. 3.1 that the simplified model with a constant hepatic glucose production term, with $n=2$, is given by

$$\begin{aligned} \dot{G}(t)= & {} G_{in} - a_1 G(t) - a_2 G(t) I(t) + C,\nonumber \\ \dot{I}(t)= & {} b_1 G(t-\tau )^2 - b_2 I(t), \quad \tau = \tau _1. \end{aligned}$$

(25)

Defining $X(t) = X = G(t) - \bar{G}$, $Y(t) = Y = I(t) - \bar{I}$, as deviations from the positive equilibrium, substituting in (25) and eliminating Y allows us to write the following nonlinear second-order DDE for X

$$\begin{aligned}&\left( \bar{G}+X \right) \ddot{X} -\dot{X}^2 + \left( a_0 + b_2 (\bar{G}+ X )\right) \dot{X} \nonumber \\&\quad +\left( \bar{G}+X \right) \left( \left( a_1+a_2 \bar{I} \right) b_2 X + a_2 b_1 \left( \bar{G}+X \right) X_{\tau } \left( 2 \bar{G}+X_{\tau }\right) \right) = 0. \end{aligned}$$

(26)

We now introduce the bifurcation parameter $\epsilon$, which is defined as the distance from the critical delay $\tau _{0}$ as $\epsilon = \sqrt{\tau - \tau _{0}}$. The variables are scaled as

$$\begin{aligned} X(t) = \epsilon u(s), \quad s = \Omega \left( \epsilon \right) t, \end{aligned}$$

(27)

where s corresponds to a new time variable ensuring that u(s) has a period of $2\pi$. Here, $\Omega$ is also assumed to have an $\epsilon$-expansion

$$\begin{aligned} \Omega = \omega _0 + \epsilon \omega _1 + \epsilon ^2 \omega _2 + \epsilon ^3 \omega _3 + \cdots , \end{aligned}$$

(28)

where $\omega _0$ is the frequency associated to the critical value $\tau _0$. Finally, we expand the delayed term $u_{\tau }$

$$\begin{aligned} u(s-\Omega \tau )&= u(s-\tau _{0} \omega _0)-\tau _{0} \omega _1 \epsilon \dot{u}(s-\tau _{0} \omega _0) \nonumber \\&\quad +\epsilon ^2 \left( \frac{1}{2} \tau _{0}^2 \omega _1^2 \ddot{u}(s-\tau _{0} \omega _0)- \dot{u}(s-\tau _{0} \omega _0)(\omega _0 +\tau _{0} \omega _2)\right) +O(\epsilon ^3), \end{aligned}$$

(29)

along with u and its derivatives

$$\begin{aligned} u(s)&= u_0(s)+\epsilon u_1(s)+\epsilon ^2 u_2(s) + \cdots , \end{aligned}$$

(30)

Substituting in (26) and collecting terms (up to and including $O(\epsilon ^2)$) gives

$$\begin{aligned}&\omega _0^2 \ddot{u}_0 +\dot{u}_0 \omega _0 (a_2 \bar{I}+a_1+b_2)+b_2 u_0 (a_2 \bar{I}+a_1) + 2 a_2 b_1 \bar{G}^2 u_{0 \tau } =0, \end{aligned}$$

(31)

$$\begin{aligned}&\omega _0^2 \ddot{u}_1 +\dot{u}_1 \omega _0 (a_2 \bar{I}+a_1+b_2)+b_2 u_1 (a_2 \bar{I}+a_1) + 2 a_2 b_1 \bar{G}^2 u_{1 \tau } \nonumber \\&\quad + \bar{G}^{-1}(u_0 (4 a_2 b_1 \bar{G}^2 u_{0 \tau }+\omega _0 (b_2 \dot{u}_0+\omega _0 \ddot{u}_0) -2 a_2 b_1 \bar{G}^3 \omega _1 \tau _0 \dot{u}_{0 \tau })+a_2 b_1 \bar{G}^2 u_{0 \tau }^2 \nonumber \\&\quad +a_2 \bar{G}\bar{I}\omega _1 \dot{u}_0+a_1 \bar{G}\omega _1 \dot{u}_0+b_2 \bar{G}\omega _1 \dot{u}_0+2 \bar{G}\omega _1 \omega _0 \ddot{u}_0- \omega _0^2 \dot{u}_0^2 \nonumber \\&\quad +b_2 u_0^2 (a_2 \bar{I}+a_1)) = 0, \end{aligned}$$

(32)

$$\begin{aligned}&\omega _0^2 \ddot{u}_2 +\dot{u}_2 \omega _0 (a_2 \bar{I}+a_1+b_2)+b_2 u_2 (a_2 \bar{I}+a_1) + 2 a_2 b_1 \bar{G}^2 u_{2 \tau } \nonumber \\&\quad + \bar{G}^{-1} (a_2 b_1 \bar{G}^3 \omega _1^2 \tau _0^2 \ddot{u}_{0 \tau }-2 a_2 b_1 \bar{G}^3 \omega _2 \tau _0 \dot{u}_{0 \tau }-2 a_2 b_1 \bar{G}^3 \omega _1 \tau _0 \dot{u}_{1 \tau }\nonumber \\&\quad -2 a_2 b_1 \bar{G}^3 \omega _0 \dot{u}_{0 \tau } +u_0 (4 a_2 b_1 \bar{G}^2 u_{1 \tau } -4 a_2 b_1 \bar{G}^2 \omega _1 \tau _0 \dot{u}_{0 \tau } +2 a_2 b_1 \bar{G}u_{0 \tau }^2 \nonumber \\&\quad + 2 b_2 u_1 (a_2 \bar{I}+a_1) +b_2 \omega _1 \dot{u}_0 +b_2 \dot{u}_1 \omega _0+2 \omega _1 \omega _0 \ddot{u}_0+\omega _0^2 \ddot{u}_1) \nonumber \\&\quad +2 a_2 b_1 \bar{G}^2 u_{0 \tau } (u_{1 \tau } -\omega _1 \tau _0 \dot{u}_{0 \tau } +2 u_1)+2 a_2 b_1 \bar{G}u_0^2 u_{0 \tau } +a_2 \bar{G}\bar{I}\omega _2 \dot{u}_0 \nonumber \\&\quad +a_2 \bar{G}\bar{I}\omega _1 \dot{u}_1+a_1 \bar{G}\omega _2 \dot{u}_0+a_1 \bar{G}\omega _1 \dot{u}_1+b_2 \bar{G}\omega _2 \dot{u}_0+b_2 \bar{G}\omega _1 \dot{u}_1+b_2 u_1 \dot{u}_0 \omega _0 \nonumber \\&\quad +2 \bar{G}\omega _2 \omega _0 \ddot{u}_0 +2 \bar{G}\omega _1 \omega _0 \ddot{u}_1+\bar{G}\omega _1^2 \ddot{u}_0-2 \omega _1 \dot{u}_0^2 \omega _0+u_1 \omega _0^2 \ddot{u}_0-2 \dot{u}_0 \dot{u}_1 \omega _0^2) = 0,\nonumber \\ \end{aligned}$$

(33)

with $u_{i \tau } = u_i (s - \tau _0 \omega _0)$. Without loss of generality, the seed solution is chosen as $u_0(s) = A_0 \cos (s)$ where, following (27), $A_0$ is related to the amplitude of X (denoted by $\bar{A}$) by $\bar{A} = A_0 \epsilon$. Choosing

$$\begin{aligned} u_1(s) = A_1 \sin (s) + B_1 \cos (s) + C_1 \sin (2s) + D_1 \cos (2s) + E_1, \end{aligned}$$

(34)

and substituting in (32) and comparing coefficients of the $\cos (s)$ and $\sin (s)$ terms shows that: (1) $A_1$, $B_1$ are arbitrary (2) $\omega _1 = 0$. From comparison of the $\cos (2s)$ and $\sin (2s)$ coefficients, it can be shown that

$$\begin{aligned} C_1&= \frac{A_0^2 F}{G}, \quad D_1 = \frac{A_0^2 H}{K}, \quad E_1 = \frac{A_0^2 (2 a_1 b_2-a_2 (2 b_1 \bar{G}^2-2 b_2 \bar{I}))}{4 \bar{G}(a_2 (2 b_1 \bar{G}^2+b_2 \bar{I})+a_1 b_2)}, \end{aligned}$$

where F, G, H and K are some functions of $a_1,a_2,b_1,b_2,\bar{G},\bar{I},\omega _0$. Due to their length, they are not reproduced here. By substituting

$$\begin{aligned} u_2(s)&= A_2 \sin (s) + B_2 \cos (s) + C_2 \sin (2s) + D_2 \cos (2s) \nonumber \\&\quad + E_2 \sin (3s) + F_2 \cos (3s) + G_2 \end{aligned}$$

(35)

along with lower-order terms into (33), and comparing the coefficients of the $\cos (s)$ and $\sin (s)$ terms, the dominant term for the amplitude, $\bar{A}$, of the limit cycle is expressible as

$$\begin{aligned} \bar{A}^2 = \frac{8 \bar{G}^2 \rho \left( 2 a_2 b_1 \bar{G}^3+a_0 b_2\right) \left( a_0^2+\bar{G}^2 \left( b_2^2+2 \rho \right) \right) p_1}{\sum _{m=0}^{7} (p_{2,m}+ \tau _0 p_{3,m}) a_0^m}\epsilon ^2, \end{aligned}$$

(36)

while the dominant term of the amplitude of the insulin oscillations, $\bar{B}$, and the second-order term for frequency correction, $\omega _2$, are given by

$$\begin{aligned} \bar{B} = \frac{\bar{A}}{a_2 \bar{G}} \sqrt{\rho + \frac{a_0^2}{\bar{G}^2}}, \quad \omega _2 = \frac{-\sqrt{\rho } \sum _{m=0}^{7} p_{3,m} a_0^m}{\sum _{m=0}^{7} (p_{2,m}+ \tau _0 p_{3,m}) a_0^m}. \end{aligned}$$

(37)

Here, we introduced the following definitions

$$\begin{aligned} \rho&= \, \omega _0^2, \\ p_1&= \, 4 a_2 b_1 \bar{G}^3 \left( b_2^3 \left( a_0^3+3 a_0 \bar{G}^2 \rho \right) +3 a_0 b_2 \rho \left( a_0^2+3 \bar{G}^2 \rho \right) -4 \bar{G}^3 \rho ^3\right) \\&\quad +b_{\rho }^2 \left( a_0^2+\bar{G}^2 \rho \right) ^2 +4 a_2^2 b_1^2 \bar{G}^6 b_{4 \rho } \left( a_0^2+4 \bar{G}^2 \rho \right) , \\ p_{2,0}&= \, 16 a_2 b_1 b_2 \bar{G}^9 \rho ^2 \left( 8 a_2^2 b_1^2 \bar{G}^4 b_{4 \rho }-2 a_2 b_1 \bar{G}^2 \left( 5 b_2^2 \rho +b_2^4+12 \rho ^2\right) +\rho b_{\rho }^2\right) , \\ p_{2,1}&= \, 2 \bar{G}^6 \rho (64 a_2^3 b_1^3 \bar{G}^6 (2 b_2^2+3 \rho ) b_{4 \rho }-4 a_2^2 b_1^2 \bar{G}^4 \rho (59 b_2^2 \rho -5 b_2^4+92 \rho ^2) \\&\quad +a_2 b_1 \bar{G}^2 \rho (59 b_2^2 \rho ^2+12 b_2^4 \rho +7 b_2^6+22 \rho ^3)-2 b_2^2 \rho ^2 b_{\rho }^2), \\ p_{2,2}&= \, b_2 \bar{G}^5 \rho (320 a_2^3 b_1^3 \bar{G}^6 b_{4 \rho }+4 a_2^2 b_1^2 \bar{G}^4 (97 b_2^2 \rho +31 b_2^4+6 \rho ^2) \\&\quad +2 a_2 b_1 \bar{G}^2 \rho (b_2^4+39 \rho ^2)-\rho (3 b_2^2+2 \rho ) b_{\rho }^2), \\ p_{2,3}&= \, \bar{G}^4 (16 a_2^3 b_1^3 \bar{G}^6 (3 b_2^2+2 \rho ) b_{4 \rho }+4 a_2^2 b_1^2 \bar{G}^4 \rho (85 b_2^2 \rho +43 b_2^4-38 \rho ^2) \\&\quad +2 a_2 b_1 \bar{G}^2 \rho (28 b_2^2 \rho ^2-59 b_2^4 \rho -7 b_2^6+44 \rho ^3)-11 b_2^2 \rho ^2 b_{\rho }^2), \\ p_{2,4}&= \, 2 b_2 \bar{G}^3 (24 a_2^3 b_1^3 \bar{G}^6 b_{4 \rho }+2 a_2^2 b_1^2 \bar{G}^4 (21 b_2^2 \rho +9 b_2^4+16 \rho ^2) \\&\quad -a_2 b_1 b_2^2 \bar{G}^2 \rho (7 b_2^2+59 \rho )-\rho (3 b_2^2+2 \rho ) b_{\rho }^2), \\ p_{2,5}&= \, 2 \bar{G}^2 (6 a_2^2 b_1^2 \bar{G}^4 (5 b_2^2 \rho +3 b_2^4-6 \rho ^2)-5 b_2^2 \rho b_{\rho }^2 \\&\quad +a_2 b_1 \bar{G}^2 \rho (11 b_2^2 \rho -15 b_2^4+22 \rho ^2)), \\ p_{2,6}&= \, - b_2 \bar{G}(6 a_2 b_1 \bar{G}^2 \rho (5 b_2^2+\rho )+(3 b_2^2+2 \rho ) b_{\rho }^2), \\ p_{2,7}&= \, -3 b_2^2 b_{\rho }^2, \\ p_{3,0}&= \, 16 a_2 b_1 \bar{G}^9 \rho ^2 b_{\rho } (8 a_2^2 b_1^2 \bar{G}^4 b_{4 \rho }-12 a_2 b_1 \bar{G}^2 \rho ^2+\rho b_{\rho }^2), \\ p_{3,1}&= \, -4 b_2 \bar{G}^6 \rho ^2 b_{\rho } (2 a_2^2 b_1^2 \bar{G}^4 (\rho -5 b_2^2)-24 a_2 b_1 \bar{G}^2 \rho ^2+\rho b_{\rho }^2), \\ p_{3,2}&= \, 2 a_2 b_1 \bar{G}^7 \rho b_{\rho } (160 a_2^2 b_1^2 \bar{G}^4 b_{4 \rho }-156 a_2 b_1 \bar{G}^2 \rho ^2+\rho (-28 b_2^2 \rho +b_2^4+31 \rho ^2)), \\ p_{3,3}&= \, b_2 \bar{G}^4 \rho b_{\rho } (4 a_2^2 b_1^2 \bar{G}^4 (43 b_2^2+85 \rho )+132 a_2 b_1 \bar{G}^2 \rho ^2-11 \rho b_{\rho }^2), \\ p_{3,4}&= \, 2 a_2 b_1 \bar{G}^5 b_{\rho } (24 a_2^2 b_1^2 \bar{G}^4 b_{4 \rho }+\rho (36 a_2 b_1 \bar{G}^2 \rho -59 b_2^2 \rho -7 b_2^4+38 \rho ^2)), \\ p_{3,5}&= \, 2 b_2 \bar{G}^2 b_{\rho } (6 a_2^2 b_1^2 \bar{G}^4 (3 b_2^2+5 \rho )+18 a_2 b_1 \bar{G}^2 \rho ^2-5 \rho b_{\rho }^2), \\ p_{3,6}&= \, 30 a_2 b_1 \bar{G}^3 \rho (\rho -b_2^2) b_{\rho }, \\ p_{3,7}&= \, -3 b_2 b_{\rho }^3, \end{aligned}$$

with $b_{\rho } = b_2^2 + \rho$ and $b_{4\rho } = b_2^2 + 4\rho$. The period of the limit cycle, T, is given by

$$\begin{aligned} T = \frac{2 \pi }{\omega _0 + \epsilon ^2 \omega _2}. \end{aligned}$$

(38)

Simulations making use of expressions (36), (37), and (38) are presented in Sect. 5.1.

4.2 Linear Hepatic Glucose Production

We now turn to study the effect of a non-constant hepatic glucose production, and hence a second delay, on the limit cycles (see model (12)). As described earlier, the P–L method has been used in a limited number of studies to investigate the effect of model parameters on the amplitude of the resulting oscillatory solutions. For example, in Brandt et al. (2006) a coupled first-order DDE model describing a two-neuron system with delay was explored. While the system had two separate delays, these were combined giving a characteristic equation of the form

$$\begin{aligned} \lambda ^2 + A_1 \lambda + A_2 + A_3 e^{- \lambda \tau } = 0, \quad \tau = \tau _1 + \tau _2, \end{aligned}$$

with $A_1, A_2$ constant and $A_3$ a function of the model parameters. In contrast, the characteristic equation of model (9), given by (15), contains a second exponential term which leads to additional challenges in finding points of bifurcation, as discussed in Sect. 3.3. For conciseness and in order to avoid the blow-up of solutions in finite time, we assume that $p=1$ although the technique can be applied to higher orders under some restrictions (see Appendix 1). The resulting equations are thus given by

$$\begin{aligned} \dot{G}(t)= & {} a_0 - a_1 G(t) - a_2 G(t) I(t) - a_3 I(t- \kappa \tau ), \end{aligned}$$

(39)

$$\begin{aligned} \dot{I}(t)= & {} b_1 G(t-\tau )^2 - b_2 I(t), \end{aligned}$$

(40)

where the dimensionless parameter $\kappa$ is used to represent the commensurateness of the time delays. In line with the calculation in the previous section, we introduce $X = G(t) - \bar{G}, Y = I(t) - \bar{I}$. Let $(\omega _0,\tau _0)$ be a critical pair obtained using the algorithm described in Sect. 3.3. Then by setting $\epsilon = \sqrt{\tau -\tau _0}$, we can scale the variables X and Y as $X(t) = \epsilon u(s), Y(t) = \epsilon v(s),$ where s is the scaled time variable as defined in (27). The expansions for v(s) and $v(s - \kappa \Omega \tau )$ are given by

$$\begin{aligned} v(s - \kappa \Omega \tau )&= v(s-\kappa \tau _0 \omega _0)-\kappa \tau _0 \omega _1 \epsilon \dot{v}(s-\kappa \tau _0 \omega _0) \nonumber \\&\quad +\frac{1}{2} \kappa \epsilon ^2 (\tau _0 (\kappa \tau _0 \omega _1^2 \ddot{v}(s-\kappa \tau _0 \omega _0)-2 \omega _2 \dot{v}(s-\kappa \tau _0 \omega _0)) \nonumber \\&\quad -2 \omega _0 \dot{v}(s-\kappa \tau _0 \omega _0)) +O(\epsilon ^3), \end{aligned}$$

(41)

$$\begin{aligned} v(s)&= v_0 (s) + \epsilon v_1 (s) + \epsilon ^2 u_2 (s) + \cdots \end{aligned}$$

(42)

Substituting in (39) and collecting terms (up to and including $O(\epsilon ^3)$) gives

$$\begin{aligned} \frac{d u_m}{ds}&= -\frac{(a_1 + a_2 \bar{I})}{\omega _0} u_m - \frac{a_2 \bar{G}}{\omega _0} v_m - \frac{a_3}{\omega _0} v_{m\tau } + g_m, \end{aligned}$$

(43)

$$\begin{aligned} \frac{d v_m}{ds}&= -\frac{b_2}{\omega _0} v_m + \frac{2 b_1 \bar{G}}{\omega _0} u_{m\tau } + h_m, \end{aligned}$$

(44)

with $m = 0,1,2$, $u_{m \tau } = u_m (s - \tau _0 \omega _0)$, $v_{m \tau } = v_m (s - \kappa \tau _0 \omega _0)$ and where the inhomogeneous terms $g_m$ and $h_m$ are related to the solutions of previous orders. Here we have $g_0 =0$, $h_0 =0$, and

$$\begin{aligned} g_1&= - a_2 u_0 v_0 + a_3 k \omega _1 \tau _{0} \dot{v_{0 \tau }} - \omega _1 \dot{u_0}, \end{aligned}$$

(45)

$$\begin{aligned} h_1&= b_1 u_{0 \tau }{}^2 - 2 b_1 \bar{G}\omega _1 \tau _{0} \dot{u_{0 \tau }} - \omega _1 \dot{v_0}, \end{aligned}$$

(46)

$$\begin{aligned} g_2&= - a_2 u_1 v_0 - a_2 u_0 v_1 -\frac{1}{2} a_3 k^2 \omega _1^2 \tau _{0}^2 \ddot{v_{0 \tau }}+a_3 \kappa \omega _1 \tau _{0} \dot{v_{1 \tau }}+a_3 \kappa \omega _0 \dot{v_{0 \tau }} \nonumber \\&\quad + a_3 \kappa \omega _2 \tau _{0} \dot{v_{0 \tau }} -a_3 v_{2 \tau }+\omega _1 \dot{u_1}-\omega _2 \dot{u_0}, \end{aligned}$$

(47)

$$\begin{aligned} h_2&= 2 b_1 u_{0 \tau } \left( u_{1 \tau }-\omega _1 \tau _{0} \dot{u_{0 \tau }}\right) -2 b_1 \bar{G}\omega _1 \tau _{0} \dot{u_{1 \tau }}-2 b_1 \bar{G}\omega _0 \dot{u_{0 \tau }}-2 b_1 \bar{G}\omega _2 \tau _{0} \dot{u_{0 \tau }} \nonumber \\&\quad + b_1 \bar{G}\omega _1^2 \tau _{0}^2 \ddot{u_{0 \tau }} - \omega _1 \dot{v_1} - \omega _2 \dot{v_0}. \end{aligned}$$

(48)

By imposing the initial conditions $u_0 (0) = C_0$, $v_0 (0) = C_0 R_1$ on the solutions of (43) and (44), with $m = 0$ we find that

$$\begin{aligned} u_0 (s) = C_0 \cos (s), \quad v_0 (s) = C_0 R_1 \cos (s) + C_0 R_2 \sin (s), \end{aligned}$$

where

$$\begin{aligned} R_1&= \, \frac{1}{Q}(-\omega _0 (a_1+a_2 \bar{I}-b_2)+a_1 b_2-2 a_2 b_1 \bar{G}^2 \sin (\tau _0 \omega _0)+2 a_2 b_1 \bar{G}^2 \cos (\tau _0 \omega _0) \\&\quad +a_2 b_2 \bar{I}+2 a_3 b_1 \bar{G}\sin ((\kappa -1) \tau _0 \omega _0)+2 a_3 b_1 \bar{G}\cos ((\kappa +1) \tau _0 \omega _0)-\omega _0^2), \\ R_2&= \, \frac{1}{Q}(\omega _0 (a_1+a_2 \bar{I}+b_2)+a_1 b_2-2 a_2 b_1 \bar{G}^2 \sin (\tau _0 \omega _0)+2 a_2 b_1 \bar{G}^2 \cos (\tau _0 \omega _0) \\&\quad +a_2 b_2 \bar{I}-2 a_3 b_1 \bar{G}\sin ((\kappa +1) \tau _0 \omega _0)+2 a_3 b_1 \bar{G}\cos ((\kappa -1) \tau _0 \omega _0)+\omega _0^2), \\ Q&= \, 2 (\omega _0 (a_2 \bar{G}+a_3 \cos (\kappa \tau _0 \omega _0))+a_3 b_2 \sin (\kappa \tau _0 \omega _0)). \end{aligned}$$

We note that $C_0$ is related to the amplitude of X(t) (denoted by $\bar{C}$) by $\bar{C} = C_0 \epsilon$ and that the amplitude of Y(t) (denoted by $\bar{D}$) is given by

$$\begin{aligned} \bar{D} = \bar{C} \sqrt{R_1^2 + R_2^2}. \end{aligned}$$

(49)

As we necessitate that the solutions $u_m$ and $v_m$ are periodic in s with period $2\pi$, we must find conditions such that the inhomogeneities do not contain secular terms. Hence, we proceed as in Brandt et al. (2006) and expand $u_m$, $v_m$, $g_m$ and $h_m$ as Fourier series to get

$$\begin{aligned} \begin{pmatrix} u_m (s) \\ v_m (s) \end{pmatrix}&= \sum _{k = 0}^{\infty } \left( \begin{pmatrix} a_{1,k}^{(m)} \\ a_{2,k}^{(m)} \end{pmatrix} \cos (k s) + \begin{pmatrix} b_{1,k}^{(m)} \\ b_{2,k}^{(m)} \end{pmatrix} \sin (k s) \right) , \end{aligned}$$

(50)

$$\begin{aligned} \begin{pmatrix} g_m (s) \\ h_m (s) \end{pmatrix}&= \sum _{k = 0}^{\infty } \left( \begin{pmatrix} \alpha _{1,k}^{(m)} \\ \alpha _{2,k}^{(m)} \end{pmatrix} \cos (k s) + \begin{pmatrix} \beta _{1,k}^{(m)} \\ \beta _{2,k}^{(m)} \end{pmatrix} \sin (k s) \right) . \end{aligned}$$

(51)

Substituting (50) and (51) in (43) and (44), it can be seen that the coefficients, $\alpha _{j,1}^{(m)}$, $\beta _{j,1}^{(m)}$ (with $j = 1,2$), in the inhomogeneities $g_m$ and $h_m$ must satisfy the following conditions

$$\begin{aligned} -a_2 \alpha _{2,1}^{(m)} \bar{G}+ \alpha _{1,1}^{(m)} b_2 - \alpha _{2,1}^{(m)} a_3 \cos (\tau _0 \omega _0) + a_3 \beta _{2,1}^{(m)} \sin (\tau _0 \omega _0) + \beta _{1,1}^{(m)} \omega _0 = 0, \end{aligned}$$

(52)

$$\begin{aligned} -\alpha _{1,1}^{(m)} \omega _0 - a_2 \beta _{2,1}^{(m)} \bar{G}+ b_2 \beta _{1,1}^{(m)} - \alpha _{2,1}^{(m)} a_3 \sin (\tau _0 \omega _0) - a_3 \beta _{2,1}^{(m)} \cos (\tau _0 \omega _0) = 0. \end{aligned}$$

(53)

The system for $k=1$ leads to equations of the form

$$\begin{aligned} C_0 \omega _1 Z_1 (a_1,a_2,a_3,b_1,b_2,\kappa ,\bar{G},\bar{I},\omega _0,\tau _0) = 0, \end{aligned}$$

(54)

$$\begin{aligned} C_0 \omega _1 Z_2 (a_1,a_2,a_3,b_1,b_2,\kappa ,\bar{G},\bar{I},\omega _0,\tau _0) = 0, \end{aligned}$$

(55)

where $Z_1, Z_2$ are functions of $a_1,a_2,a_3,b_1,b_2,\kappa ,\bar{G},\bar{I},\omega _0,\tau _0$. If $C_0 = 0$, then we obtain the trivial solution. Additionally, it can be seen that $Z_1$ and $Z_2$ do not vanish modulo the characteristic curve. Therefore, following our assumption that $\omega _0$ does not satisfy any polynomial equation of lower order, this implies that $\omega _1=0$. For further details of the derivation of these conditions, the reader is referred to Appendix 1. Substituting these conditions in (43) and (44) leads to the following expressions

$$\begin{aligned} u_1 (s)&= a_{1,0}^{(1)} + a_{1,1}^{(1)} \cos (s) + b_{1,1}^{(1)} \sin (s) + C_0^2 h_1 \cos (2 s) + C_0^2 h_2 \sin (2 s),\end{aligned}$$

(56)

$$\begin{aligned} v_1 (s)&= a_{2,0}^{(1)} + a_{2,1}^{(1)} \cos (s) + b_{2,1}^{(1)} \sin (s) + C_0^2 h_3 \cos (2 s) + C_0^2 h_4 \sin (2 s), \end{aligned}$$

(57)

where $h_1, h_2, h_3$ and $h_4$ are functions of $a_1, a_2, a_3, b_1, b_2, \kappa , \bar{G}, \bar{I}, \omega _0, \tau _0$. Expressions for $\alpha _{1,1}^{(2)}$, $\beta _{1,1}^{(2)}$, $\alpha _{1,2}^{(2)}$ and $\beta _{1,2}^{(2)}$ can then be obtained. Finally, using conditions (52), (53) and solving the resulting system of equations, it can be shown that the dominant term for the amplitude, $\bar{C}$, the second-order term for frequency correction, $\omega _2$, and the period, T, can be expressed as

$$\begin{aligned} \bar{C}^2 = \frac{W_1}{V_1} \epsilon ^2, \quad \omega _2 = \frac{W_2}{V_2}, \quad T = \frac{2 \pi V_2}{\omega _0 V_2 + W_2 \epsilon ^2}, \end{aligned}$$

(58)

where $W_1$, $W_2$, $V_1$ and $V_2$ are functions of $a_1$, $a_2$, $a_3$, $b_1$, $b_2$, $\bar{G}$, $\bar{I}$, $\kappa$, $\omega _0$ and $\tau _0$. Given their length, the expressions are not reproduced here but are used in simulations in Sect. 5.2.

5 Parameter Analysis

The closed-form expressions for the limit cycles presented in this paper allow for the effect of changes in each of the model parameters on the amplitude and period to be more easily studied. In this section, we first study the effect of changes in $a_2$ (insulin resistance), $b_1$ (insulin secretion) and $b_2$ (insulin degradation) on the important characteristics of the waveforms for the constant hepatic production model solutions. Secondly, we investigate how the amplitude and period of the solutions of model (39) vary with respect to the delay coupling parameter $\kappa$.

5.1 Constant Hepatic Glucose Production

In this section, the closed-form expressions for the amplitude and period of the solutions to model (3), as given by (36), (37) and (38), will be analysed using two different Parameter Sets, which are given in Table 2. The values used in Parameter Set 1 are based off the values used in Huard et al. (2015), Li et al. (2006) and Sturis et al. (1991) and represent a patient under a constant glucose infusion, while Parameter Set 2 looks to replicate the values that may be observed in a patient under a larger constant glucose infusion.

Table 2 Parameter Sets 1 and 2 which are used in numerical simulations throughout Sect. 5.1

5.1.1 On the Influence of Insulin Sensitivity

To begin, we analysed the relationship between the insulin sensitivity parameter $a_2$ and the closed-form expressions for the amplitude and period of model (3). It can be seen from Fig. 4 that the amplitude of X(t), as given by (36), varies between 4 and 15 for Parameter Set 1, and 1 and 38 mg/dl for Parameter Set 2. Additionally, the amplitude of Y(t) from (37) is observed to be approximately between either 1 and 5, or 1 and 29 mU/l. These values are within a physiologically acceptable range. Furthermore, in Fig. 5 we note that the values of the period, as defined by (38), vary between 74.5 and 76 minutes for Parameter Set 1, and 76 and 78 min for Parameter Set 2, and hence are also within an acceptable range. It can be seen in Fig. 6 that increasing $a_2$ has little effect on the oscillations, while decreasing $a_2$ has a more profound effect. For example, for Parameter Set 1 a $20\%$ increase in $a_2$ from 0.0017 increases the amplitude by $15\%$. However, a $20\%$ decrease in $a_2$ reduces the amplitude by almost $80\%$. Similarly for Parameter Set 2, a $20\%$ increase in $a_2$ from 0.0004 increases the amplitude by less than $5\%$ while a $20\%$ decrease in $a_2$ reduces the amplitude by approximately $30\%$.

Fig. 4

Amplitudes of the oscillations, $\bar{A}$ and $\bar{B}$, as a function of $a_2$ using Parameter Set 1 (left) and Parameter Set 2 (right)

Fig. 5

Period of the oscillations, as given by (38), as a function of $a_2$ using Parameter Set 1 (left) and Parameter Set 2 (right)

Fig. 6

Percentage change of the closed-form expressions of the amplitude (blue) and period (black) of Y(t), which are given by (37) and (38) respectively, versus the percentage change in $a_2$ for Parameter Set 1 (left) and Parameter Set 2 (right). The initial value used for $a_2$ was: 0.0017 (left); and 0.0004 (right)

5.1.2 Insulin Secretion Capacity $b_1$ and Insulin Degradation $b_2$ versus $\bar{A}$ and $\bar{B}$

Next, we looked at the relationship between the insulin secretion capacity $b_1$ and the closed-form expression of the amplitude of X(t) defined by (36). As shown in Fig. 7a, the amplitude variation with respect to $b_1$ is between 0 and 19, regardless of the value of $a_2$ used. However, $a_2$ does have an effect on the decline of amplitude observed with an increased $b_1$. Indeed as $a_2$ increases, the observed value of $b_1$ such that the amplitude begins to decrease decreases. This effect is also observed in Fig. 7b.

Fig. 7

Amplitude of X(t), as given by (36), and Y(t), as given by (37), versus $b_1$ and $b_2$ for Parameter Sets 1 and 2

Figure 7c, d show the effect of $b_2$ on the amplitude of X(t) and Y(t) respectively for Parameter Set 1. It is observed from both that the oscillations are lost when $b_2$ drops below $\approx 0.059$ regardless of the value of $a_2$. Indeed, when looking at the amplitude as a function of $b_2$, $a_2$ has very little effect on $\bar{A}$ and only a small effect on $\bar{B}$ for Parameter Set 1. However, as seen in Fig. 7e, f, this is not true for Parameter Set 2, where $a_2$ has a more profound effect on both the amplitude of X(t) and Y(t). Irrespective of this, it is observed for both Parameter Sets that an increase in $b_2$ leads to an increase in the amplitude of the oscillations. While the size of the oscillations of Y(t) in Fig. 7d, f is plausible for all values of $b_2$, the size of the oscillations in Fig. 7c, e becomes too large with $b_2$. Indeed, eventually the value of $\bar{G}- \bar{A}$ drops below 70 mg/dl in both cases. Physiologically, this would mean the onset of hypoglycaemia. The ranges $0.06< b_2 < 0.062$ for Parameter Set 1, and $0.064< b_2 < 0.075$ for Parameter Set 2 ensure that glucose levels are kept within a realistic physiological range.

5.2 Non-constant Hepatic Glucose Production

We now move on to investigate the effect of the two delays on the closed-form expressions for the amplitude and period of model (39). In particular, we focus on the relationship between the amplitudes of X(t) and Y(t), given by (58) and (49) respectively, and the commensurate delay parameter $\kappa$. Using Parameter Set 1 with $a_2 = 0.0017$, it can be seen in Fig. 8 that when $a_3$ is small, $\kappa$ has a negligible effect on the amplitude. Additionally, when $a_3 < O(10^{-2})$, changes in $a_3$ also have a negligible effect on the amplitudes. However, when $a_3 = 0.1$ it is observed that the amplitude of both X(t) and Y(t) varies with $\kappa$ in an oscillatory manner.

To further investigate how the closed-form expressions for the amplitude and period vary with $\kappa$, we now look into the variation using the parameter values given in Table 3. From Fig. 9, we can see that $\kappa$ has a large influence on both the amplitude and period for Parameter Set 3. Increasing $\kappa$ from 1 to 7, the amplitude increases by $\approx 700 \%$ and the period by $\approx 500 \%$. However, it must be noted that for $\kappa > 1$ the values of the amplitude and period are not in a physiological range. This is most likely due to the size of $\epsilon ^2$. Indeed, when $\kappa = 7$ we note that $\epsilon ^2 = 9.49476$ compared with 0.2806 when $\kappa =1$. Therefore, instead of setting $\tau = 16$ we shall instead choose $\tau$ such that $\epsilon ^2 = 0.16$. The results can be seen in Fig. 10. Here we observe that the amplitude remains in a physiological range for $1 \le \kappa \le 7$ and that the period of the oscillations is within an acceptable physiological range for insulin levels. We also note that there is very little variation in the amplitude when $\kappa$ increases. This implies that more accurate values of the two delays can be chosen without losing the physiological accuracy of the oscillations.

Fig. 8

Amplitude of X(t) (left) and Y(t) (right), as defined by (58) and (49) respectively, as a function of $\kappa$ for Parameter Set 1 with $a_2 = 0.0017$

Table 3 Parameter Set 3

6 Discussion

In this contribution, we have analysed two polynomial DDE models of the glucose–insulin regulatory system, one with a constant hepatic glucose production and one with a linear hepatic production containing a commensurate delay, to investigate the effect of various diabetic parameters on the ultradian oscillations. Indeed, by performing a P–L perturbation method we have been able to obtain analytical expressions that are based on the model parameters for the linearised amplitude and period of the two models.

From a mathematical point of view, the accuracy of these expressions is of a high degree. Indeed, from Fig. 11 we can see that the closed-form expression for the amplitude of X(t) given by (36) is almost an exact match for the amplitude obtained through numerical simulations. Furthermore, Fig. 12 shows that the first-order solutions for G(t) and I(t) of (3) obtained using the P–L technique are a good approximation to the solutions calculated using a classical Runge–Kutta method. Increasing the accuracy by taking into account the second and third-order terms computed in Sect. 4 leads to an approximate solution that is indistinguishable from the one obtained numerically.

Fig. 9

Amplitude of X(t) (left) and Y(t) (right), as defined by (58) and (49) respectively, versus $\kappa$ for Parameter Set 3

Fig. 10

Amplitude of X(t) (left) and Y(t) (right), as given by (58) and (49) respectively, versus $\kappa$ for fixed $\epsilon$. All other parameters are as defined in Table (3)

Fig. 11

Comparison of two methods for calculating the amplitude of X(t) from model (3) using Parameter Set 1. The blue line represents the P–L approximation given by (36), and the black dots represent the numerical approximations obtained using a Runge–Kutta method

Fig. 12

Comparison of the limit cycles corresponding to the linear approximation given by (36), (37) and (38), and the numerical solution of system (3). Parameter values are as defined in Parameter Set 1, with $a_2 = 0.002$

From a physiological perspective, it is important to note while the values of the amplitude of X(t) in Fig. 4 are within a physiologically acceptable range, the decrease in amplitude in the presence of mild insulin resistance is most notably seen experimentally in insulin levels, while the amplitude in glucose oscillations has been observed to remain almost constant (O’Meara et al. 1993). Therefore, the expressions derived in this paper could theoretically be used to obtain estimates for insulin sensitivity through the matching of clinical insulin data to the two models.

Finally, we note that strategies aiming to restore glucose–insulin oscillations could make use of the fact that the amplitude and frequency of oscillations show very little variation in the vicinity of the Hopf threshold curve in the space of delays. These theoretical findings could therefore have an impact on optimal glycemic control.

Appendices

A Finite-time blow-up solutions

The introduction of an additional nonlinear term in model 9, namely

$$\begin{aligned} \dot{G} = a_0 - a_1 G - a_2 G I - a_3 I(t-\tau _2)^p, \quad \dot{I} = b_1 G(t-\tau _1)^n - b_2 I, \end{aligned}$$

(59)

when $a_3 \ne 0$ and $p>1$, can give rise to new dominant behaviour which may lead to singularities in the trajectories. In particular, the presence of poles induces a blow-up of at least one of the phase variables in finite time. Sufficient conditions for the existence of poles for which the location depends on initial conditions can be obtained by performing a local singularity analysis on each dominant nonlinear truncation of the system. Here, we restrict ourselves to system (59) without delays, for which this type of analysis is well established and commonly known as Painlevé analysis (Conte 2012; Goriely and Hyde 1998, 2000; Hone 2009).

Two nonlinear truncations of (59) can be distinguished as

$$\begin{aligned} \begin{array}{llll} A. &{} \quad \dot{G} \sim -a_2 G I\qquad \qquad &{} B. &{}\quad \dot{G} \sim -a_3 I^p, p>1. \\ &{} \quad \dot{I} \sim b_1 G^n &{} &{}\quad \dot{I} \sim b_1 G^n \end{array} \end{aligned}$$

Looking for dominant terms of the form

$$\begin{aligned} G(t) \sim \alpha _1 (t-t_0)^{q_1}, \quad I(t) \sim \alpha _2 (t-t_0)^{q_2}, \end{aligned}$$

(60)

one is led to the following solution for each truncation

$$\begin{aligned}&A.&G(t) \sim 2^{1/n} \left( \frac{-1}{n a_2 b_1}\right) ^{1/n} (t-t_0)^{-2/n},\end{aligned}$$

(61)

$$\begin{aligned}&I(t) \sim \frac{2}{a_2 n} (t-t_0)^{-1}, \end{aligned}$$

(62)

$$\begin{aligned}&B.&G(t) \sim \left( \frac{ (-1)^p a_3 b_1^p (n+1)^{-p} (n p-1)^{p+1}}{p+1}\right) ^{\frac{1}{1-n p}}(t-t_0)^{\frac{1+p}{1 - n p}}, \end{aligned}$$

(63)

$$\begin{aligned}&I(t) \sim \left( -\frac{b_1 a_3^n (p+1)^{-n} (n p-1)^{n+1}}{n+1}\right) {}^{\frac{1}{1-n p}} (t-t_0)^{\frac{1+n}{1 - n p}}. \end{aligned}$$

(64)

The following conclusions can be drawn.

Truncation A.:

Since all parameters are assumed to be strictly positive, we see that when n is even, equations (61), (62) do not lead to an expression with real coefficients. Therefore, no open set of initial conditions leads to a movable pole (Goriely and Hyde 1998, 2000).

Truncation B.:

In order to have a pole when $p>1$, the quantities $z_1=\frac{1+p}{n p-1}$ and $z_2=\frac{1+n}{n p-1}$ need to be positive integers, which can only happen when $n=p=2$. Indeed, since n is assumed to be even and $p>1$, the quantity $np-1$ is larger than 1. Hence, for $z_1$ and $z_2$ to be positive integers, one needs to have the inequalities

$$\begin{aligned} 1+n \ge n p - 1, \qquad 1+p \ge n p - 1, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} p \le \frac{2}{n} + 1 \le 2,\qquad n \le \frac{2}{p} + 1 \le 2, \end{aligned}$$

thus leading to $n=p=2$. Under these conditions, it is easily seen that the coefficients defined by equations (63), (64) are real. Further looking for additional powers in the expansion allowing for the presence of arbitrary constants (so-called resonances),

$$\begin{aligned}&G(t) \sim \alpha _1 (t-t_0)^{q_1} (1 + \delta _1 (t-t_0)^r),\\&\quad I(t) \sim \alpha _2 (t-t_0)^{q_2} (1+\delta _2 (t-t_0)^r), \end{aligned}$$

we obtain the following values for r,

$$\begin{aligned} r_0 = -1, \quad r_1 = \frac{(1+p)(1+n)}{np - 1} = 3, \end{aligned}$$

where $r_0=-1$ corresponds to the arbitrariness of $t_0$. The coefficient $r_1$ being a positive integer by construction, it provides the order at which an additional arbitrary constant may appear, which is necessary to satisfy the initial value problem.

Thus, it is shown that Truncation B (with $n=p=2$) may possess finite-time blow-up solutions. Of course, these considerations do not exclude the potential presence of other types of singularities for other values of n, p.

B Justification of Eqs. (52) and (53)

Here we show how conditions (52), (53) are obtained. First, we note that from (16) and (17) it can be seen that

$$\begin{aligned} \cos ((\kappa + 1) \omega _0 \tau _0)&= \frac{-a_5 (a_1+a_2 \bar{I})-2 a_2 a_4 \bar{G}^2 \cos (\tau _0 \omega _0)+\omega _0^2}{2 a_3 a_4 \bar{G}} , \end{aligned}$$

(65)

$$\begin{aligned} \sin ((\kappa + 1) \omega _0 \tau _0)&= \frac{\omega _0 (a_1+a_2 \bar{I}+a_5)-2 a_2 a_4 \bar{G}^2 \sin (\tau _0 \omega _0)}{2 a_3 a_4 \bar{G}} . \end{aligned}$$

(66)

Through the substitution of the Fourier series decompositions (given by (50) and (51)) into (43), (44) and comparing the coefficients of $\cos (\kappa s)$ and $\sin (\kappa s)$, we obtain that

$$\begin{aligned}&a_3 a^{(m)}_{2,k } \cos \left( k \kappa \omega _0 \tau _{0}\right) +a_1 a^{(m)}_{1,k }+a_2 \bar{G}a^{(m)}_{2,k }+a_2 \bar{I}a^{(m)}_{1,k }-a_3 b^{(m)}_{2,k } \sin \left( k \kappa \omega _0 \tau _{0}\right) \nonumber \\&\quad +k \omega _0 b^{(m)}_{1,k }-\alpha ^{(m)}_{1,k} = 0, \end{aligned}$$

(67)

$$\begin{aligned}&a_3 a^{(m)}_{2,k } \sin \left( k \kappa \omega _0 \tau _{0}\right) +a_3 b^{(m)}_{2,k } \cos \left( k \kappa \omega _0 \tau _{0}\right) +a_1 b^{(m)}_{1,k }+a_2 \bar{G}b^{(m)}_{2,k }+a_2 \bar{I}b^{(m)}_{1,k } \nonumber \\&\quad -k \omega _0 a^{(m)}_{1,k} -\beta ^{(m)}_{1,k } = 0, \end{aligned}$$

(68)

$$\begin{aligned}&a_5 a^{(m)}_{2,k} -2 a_4 \bar{G}a^{(m)}_{1,k} \cos \left( k \omega _0 \tau _{0}\right) +2 a_4 \bar{G}b^{(m)}_{1,k} \sin \left( k \omega _0 \tau _{0}\right) +k \omega _0 b^{(m)}_{2,k }-\alpha ^{(m)}_{2,k} = 0, \end{aligned}$$

(69)

$$\begin{aligned}&a_5 b^{(m)}_{2,k} -2 a_4 \bar{G}a^{(m)}_{1,k} \sin \left( k \omega _0 \tau _{0}\right) -k \omega _0 a^{(m)}_{2,k}-2 a_4 \bar{G}b^{(m)}_{1,k} \cos \left( k \omega _0 \tau _{0}\right) -\beta ^{(m)}_{2,k} = 0, \end{aligned}$$

(70)

which can then be solved for $a^{(m)}_{1,k}$, $a^{(m)}_{2,k}$, $b^{(m)}_{1,k}$ and $b^{(m)}_{2,k}$, with any inhomogeneity, when $k > 1$. The solution of (67)–(70) (for $k > 1$) is

$$\begin{aligned} a_{1,k}^{(m)}&= \, \frac{1}{D} \{-a_1 a_3 b_2 \alpha _{2,k }^{(m)} \cos (k \kappa \tau _0 \omega _0)+a_1 a_3 b_2 \beta _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0) \\&\quad -2 a_2 a_3 b_1 \bar{G}^2 \alpha _{2,k}^{(m)} \cos (k (\kappa -2) \tau _0 \omega _0) \\&\quad +2 a_2 a_3 b_1 \bar{G}^2 \beta _{2,k }^{(m)} \sin (k (\kappa -1) \tau _0 \omega _0) +k \omega _0 (a_3 b_2 \alpha _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0) \\&\quad -2 a_3 b_1 \bar{G}\alpha _{1,k }^{(m)} \sin (k (\kappa +1) \tau _0 \omega _0) +2 a_3 b_1 \bar{G}\beta _{1,k}^{(m)} \cos (k (\kappa +1) \tau _0 \omega _0) \\&\quad +a_3 \beta _{2,k}^{(m)} (a_2 \bar{I}+a_1+b_2) \cos (k \kappa \tau _0 \omega _0) -2 a_2 b_1 \bar{G}^2 \alpha _{1,k}^{(m)} \sin (k \tau _0 \omega _0) \\&\quad +2 a_2 b_1 \bar{G}^2 \beta _{1,k}^{(m)} \cos (k \tau _0 \omega _0)+a_2 \bar{G}\beta _{2,k}^{(m)} (a_2 \bar{I}+a_1+b_2) \\&\quad +a_1 a_3 \alpha _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0)+k \omega _0 (a_1 \alpha _{1,k}^{(m)}+a_3 \alpha _{2,k}^{(m)} \cos (k \kappa \tau _0 \omega _0) \\&\quad -a_3 \beta _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0) +a_2 \bar{G}\alpha _{2,k }^{(m)}+a_2 \bar{I}\alpha _{1,k}^{(m)}- k \omega _0 \beta _{1,k }^{(m)}) \\&\quad +a_2 a_3 \bar{I}\alpha _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0)-b_2^2 \beta _{1,k}^{(m)}) \\&\quad +2 a_3 b_1 \bar{G}\cos (k (\kappa +1) \tau _0 \omega _0) (b_2 \alpha _{1,k}^{(m)}-a_2 \bar{G}\alpha _{2,k}^{(m)}) \\&\quad +2 a_3 b_1 \bar{G}\sin (k (\kappa +1) \tau _0 \omega _0) (b_2 \beta _{1,k}^{(m)}-a_2 \bar{G}\beta _{2,k}^{(m)}) \\&\quad -a_2 a_3 b_2 \bar{I}\alpha _{2,k}^{(m)} \cos (k k \tau _0 \omega _0) +a_2 a_3 b_2 \bar{I}\beta _{2,k}^{(m)} \sin (k \kappa \tau _0 \omega _0) \\&\quad -2 a_2^2 b_1 \bar{G}^3 \beta _{2,k}^{(m)} \sin (k \tau _0 \omega _0)+2 a_2 b_1 b_2 \bar{G}^2 \beta _{1,k}^{(m)} \sin (k \tau _0 \omega _0) \\&\quad -2 b_1 \bar{G}\cos (k \tau _0 \omega _0) (a_3^2 \alpha _{2,k}^{(m)}+a_2 \bar{G}(a_2 \bar{G}\alpha _{2,k}^{(m)}-b_2 \alpha _{1,k}^{(m)})) \\&\quad -2 a_3^2 b_1 \bar{G}\beta _{2,k }^{(m)} \sin (k \tau _0 \omega _0) +b_2 (a_2 \bar{I}+a_1) (b_2 \alpha _{1,k}^{(m)}-a_2 \bar{G}\alpha _{2,k}^{(m)}) \}, \end{aligned}$$

$$\begin{aligned} b_{1,k}^{(m)}&= \, \frac{1}{D}\{ a_1 a_3 b_2 \alpha _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0)+a_1 a_3 b_2 \beta _{2,k }^{m} \cos (k \kappa \tau _0 \omega _0) \\&\quad +2 a_2 a_3 b_1 \bar{G}^2 \alpha _{2,k }^{m} \sin (k (\kappa -1) \tau _0 \omega _0)+2 a_2 a_3 b_1 \bar{G}^2 \beta _{2,k }^{m} \cos (k (\kappa -1) \tau _0 \omega _0) \\&\quad -k \omega _0 (a_3 b_2 \beta _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0)-2 a_3 b_1 \bar{G}\alpha _{1,k }^{m} \cos (k (\kappa +1) \tau _0 \omega _0) \\&\quad -2 a_3 b_1 \bar{G}\beta _{1,k }^{m} \sin (k (\kappa +1) \tau _0 \omega _0)-a_3 \alpha _{2,k }^{m} (a_2 \bar{I}+a_1+b_2) \cos (k \kappa \tau _0 \omega _0) \\&\quad -2 a_2 b_1 \bar{G}^2 \alpha _{1,k }^{m} \cos (k \tau _0 \omega _0)-2 a_2 b_1 \bar{G}^2 \beta _{1,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad -a_2 \bar{G}\alpha _{2,k }^{m} (a_2 \bar{I}+a_1+b_2) +a_1 a_3 \beta _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0) \\&\quad +k \omega _0 (a_1 \beta _{1,k }^{m}+k \omega _0 \alpha _{1,k }^{m}+a_3 \alpha _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0) +a_3 \beta _{2,k }^{m} \cos (k \kappa \tau _0 \omega _0) \\&\quad +a_2 \bar{G}\beta _{2,k }^{m}+a_2 \bar{I}\beta _{1,k }^{m})+a_2 a_3 \bar{I}\beta _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0)+b_2^2 \alpha _{1,k }^{m}) \\&\quad +2 a_3 b_1 \bar{G}\sin (k (\kappa +1) \tau _0 \omega _0) (b_2 \alpha _{1,k }^{m}-a_2 \bar{G}\alpha _{2,k }^{m}) \\&\quad +2 a_3 b_1 \bar{G}\cos (k (\kappa +1) \tau _0 \omega _0) (a_2 \bar{G}\beta _{2,k }^{m}-b_2 \beta _{1,k }^{m}) \\&\quad +a_2 a_3 b_2 \bar{I}\alpha _{2,k }^{m} \sin (k \kappa \tau _0 \omega _0) +a_2 a_3 b_2 \bar{I}\beta _{2,k }^{m} \cos (k \kappa \tau _0 \omega _0) \\&\quad -2 a_2^2 b_1 \bar{G}^3 \alpha _{2,k }^{m} \sin (k \tau _0 \omega _0) +2 a_2 b_1 b_2 \bar{G}^2 \alpha _{1,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad -2 a_3^2 b_1 \bar{G}\alpha _{2,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad +2 b_1 \bar{G}\cos (k \tau _0 \omega _0) (a_3^2 \beta _{2,k }^{m}+a_2 \bar{G}(a_2 \bar{G}\beta _{2,k }^{m}-b_2 \beta _{1,k }^{m})) \\&\quad +b_2 (a_2 \bar{I}+a_1) (a_2 \bar{G}\beta _{2,k }^{m}-b_2 \beta _{1,k }^{m}) \}, \end{aligned}$$

$$\begin{aligned} a_{2,k}^{(m)}&= \, \frac{1}{D}\{ 2 b_1 \bar{G}(-a_1 b_2 \beta _{1,k }^{m} \sin (k \tau _0 \omega _0) +2 a_3 b_1 \bar{G}\alpha _{1,k }^{m} \cos (k \kappa \tau _0 \omega _0) \\&\quad +2 a_3 b_1 \bar{G}\beta _{1,k }^{m} \sin (k \kappa \tau _0 \omega _0)+(a_2 \bar{I}+a_1) \cos (k \tau _0 \omega _0) (a_2 \bar{G}\alpha _{2,k }^{m}+b_2 \alpha _{1,k }^{m}) \\&\quad -a_2 b_2 \bar{I}\beta _{1,k }^{m} \sin (k \tau _0 \omega _0) +a_3 (a_2 \bar{I}+a_1) \alpha _{2,k }^{m} \cos (k (\kappa +1) \tau _0 \omega _0) \\&\quad +a_3 (a_2 \bar{I}+a_1) \beta _{2,k }^{m} \sin (k (\kappa +1) \tau _0 \omega _0) +a_1 a_2 \bar{G}\beta _{2,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad +a_2^2 \bar{G}\bar{I}\beta _{2,k }^{m} \sin (k \tau _0 \omega _0)) \\&\quad -k \omega _0 (2 b_1 \bar{G}(\sin (k \tau _0 \omega _0) (\alpha _{1,k }^{m} (a_2 \bar{I}+a_1+b_2)+a_2 \bar{G}\alpha _{2,k }^{m}) \\&\quad +\cos (k \tau _0 \omega _0) (\beta _{1,k }^{m} (a_2 \bar{I}+a_1+b_2)-a_2 \bar{G}\beta _{2,k }^{m}) \\&\quad +a_3 \alpha _{2,k }^{m} \sin (k (\kappa +1) \tau _0 \omega _0) -a_3 \beta _{2,k }^{m} \cos (k (\kappa +1) \tau _0 \omega _0)) \\&\quad +(a_2 \bar{I}+a_1){}^2 \beta _{2,k }^{m}+k \omega _0 (-b_2 \alpha _{2,k }^{m}+k \omega _0 \beta _{2,k }^{m} +2 b_1 \bar{G}\alpha _{1,k }^{m} \cos (k \tau _0 \omega _0) \\&\quad -2 b_1 \bar{G}\beta _{1,k }^{m} \sin (k \tau _0 \omega _0)))+4 a_2 b_1^2 \bar{G}^3 \alpha _{1,k }^{m}+b_2 (a_2 \bar{I}+a_1){}^2 \alpha _{2,k }^{m} \}, \end{aligned}$$

$$\begin{aligned} b_{2,k}^{(m)}&= \, \frac{1}{D} \{ 2 b_1 \bar{G}(a_1 b_2 \alpha _{1,k }^{m} \sin (k \tau _0 \omega _0)-2 a_3 b_1 \bar{G}\alpha _{1,k }^{m} \sin (k \kappa \tau _0 \omega _0) \\&\quad +2 a_3 b_1 \bar{G}\beta _{1,k }^{m} \cos (k \kappa \tau _0 \omega _0) +(a_2 \bar{I}+a_1) \cos (k \tau _0 \omega _0) (a_2 \bar{G}\beta _{2,k }^{m}+b_2 \beta _{1,k }^{m}) \\&\quad +a_2 b_2 \bar{I}\alpha _{1,k }^{m} \sin (k \tau _0 \omega _0) -a_3 (a_2 \bar{I}+a_1) \alpha _{2,k }^{m} \sin (k (\kappa +1) \tau _0 \omega _0) \\&\quad +a_3 (a_2 \bar{I}+a_1) \beta _{2,k }^{m} \cos (k (\kappa +1) \tau _0 \omega _0) -a_1 a_2 \bar{G}\alpha _{2,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad -a_2^2 \bar{G}\bar{I}\alpha _{2,k }^{m} \sin (k \tau _0 \omega _0)) \\&\quad +k \omega _0 (-2 b_1 \bar{G}(-\cos (k \tau _0 \omega _0) (\alpha _{1,k }^{m} (a_2 \bar{I}+a_1+b_2)-a_2 \bar{G}\alpha _{2,k }^{m}) \\&\quad +\sin (k \tau _0 \omega _0) (\beta _{1,k }^{m} (a_2 \bar{I}+a_1+b_2)+a_2 \bar{G}\beta _{2,k }^{m}) \\&\quad +a_3 \alpha _{2,k }^{m} \cos (k (\kappa +1) \tau _0 \omega _0)+a_3 \beta _{2,k }^{m} \sin (k (\kappa +1) \tau _0 \omega _0)) \\&\quad +(a_2 \bar{I}+a_1){}^2 \alpha _{2,k }^{m}+k \omega _0 (k \omega _0 \alpha _{2,k }^{m}+b_2 \beta _{2,k }^{m} -2 b_1 \bar{G}(\alpha _{1,k }^{m} \sin (k \tau _0 \omega _0) \\&\quad +\beta _{1,k }^{m} \cos (k \tau _0 \omega _0))))+4 a_2 b_1^2 \bar{G}^3 \beta _{1,k }^{m}+b_2 (a_2 \bar{I}+a_1){}^2 \beta _{2,k }^{m} \}, \end{aligned}$$

where

$$\begin{aligned} D&= \, k \omega _0 (-4 b_1 \bar{G}(a_2 \bar{I}+a_1+b_2) (a_3 \sin (k (\kappa +1) \tau _0 \omega _0)+a_2 \bar{G}\sin (k \tau _0 \omega _0)) \nonumber \\&\quad +k \omega _0 (-4 b_1 \bar{G}(a_3 \cos (k (\kappa +1) \tau _0 \omega _0)+a_2 \bar{G}\cos (k \tau _0 \omega _0)) \nonumber \\&\quad +(a_2 \bar{I}+a_1){}^2+b_2^2)+k ^3 \omega _0^3) +4 b_1 \bar{G}(a_2 \bar{G}(2 a_3 b_1 \bar{G}\cos (k \kappa \tau _0 \omega _0) \nonumber \\&\quad +b_2 (a_2 \bar{I}+a_1) \cos (k \tau _0 \omega _0)) +a_3 b_2 (a_2 \bar{I}+a_1) \cos (k (\kappa +1) \tau _0 \omega _0)) \nonumber \\&\quad +4 b_1^2 \bar{G}^2 (a_2^2 \bar{G}^2+a_3^2)+b_2^2 (a_2 \bar{I}+a_1){}^2. \end{aligned}$$

(71)

Note that when $k = 1$, $D = 0$, and therefore we must re-examine (67)–(70) for $k = 1$. By taking $(\omega _0$ (67) $+$$(a_2 \bar{G}+ a_3 \cos {(\kappa \tau _0 \omega _0}))$ (70)) − $(b_2$ (68) − $(a_3 \sin {(\kappa \tau _0 \omega _0}))$ (69)) we obtain (52). Similarly, by taking $(b_2$ (67) − $(a_2 \bar{G}+ a_3 \cos {(\kappa \tau _0 \omega _0)})$ (69)) $+$$(\omega _0$ (68) $+$$(a_3 \sin {(\kappa \tau _0 \omega _0})$ (70)), we obtain (53). When $k = 1$, the coefficients of the inhomogeneities $g_1$ and $h_1$ are

$$\begin{aligned} \alpha _{1,1}^{(1)}&= \frac{\kappa C_0 \tau _0 \omega _1 v_1}{v_5 \omega _0},&\quad \beta _{1,1}^{(1)} = \frac{C_0 \omega _1 (\kappa \tau _0 v_2 -2 v_1 )}{v_5 \omega _0}, \\ \alpha _{2,1}^{(1)}&= \frac{C_0 \omega _1 v_3}{v_5},&\quad \beta _{2,1}^{(1)} = \frac{C_0 \omega _1 v_4}{v_5}, \end{aligned}$$

where

$$\begin{aligned} v_1&= a_3 \omega _0 (a_2 \bar{I}+a_1-b_2) \sin (\kappa \tau _0 \omega _0)-a_3 (b_2 (a_2 \bar{I}+a_1)+\omega _0^2) \cos (\kappa \tau _0 \omega _0) \\&\quad +\bar{G}(-2 b_1 (a_3-a_2 \bar{G}) (a_2 \bar{G}+a_3) \cos (\tau _0 \omega _0)+a_2 b_2 (a_2 \bar{I}+a_1)-a_2 \omega _0^2) , \\ v_2&= \, -a_3 (b_2 (a_2 \bar{I}+a_1)+\omega _0^2) \sin (\kappa \tau _0 \omega _0)-a_3 \omega _0 (a_2 \bar{I}+a_1-b_2) \cos (\kappa \tau _0 \omega _0) \\&\quad +2 b_1 \bar{G}(a_2^2 \bar{G}^2-a_3^2) \sin (\tau _0 \omega _0)-a_2 \bar{G}\omega _0 (a_2 \bar{I}+a_1+b_2), \\ v_3&= \, 2 b_1 \bar{G}(a_3 \cos ((\kappa -1) \tau _0 \omega _0)+2 \tau _0 v_1 \sin (\tau _0 \omega _0))+a_2 (2 b_1 \bar{G}^2 \cos (\tau _0 \omega _0)+b_2 \bar{I}) \\&\quad +a_1 b_2+\omega _0^2, \\ v_4&= \, 2 b_1 \bar{G}(-a_3 \sin ((\kappa -1) \tau _0 \omega _0)+a_2 \bar{G}\sin (\tau _0 \omega _0)-2 \tau _0 v_1 \cos (\tau _0 \omega _0)) \\&\quad +\omega _0 (a_2 \bar{I}+a_1-b_2), \\ v_5&= \, 2 (a_3 b_2 \sin (\kappa \tau _0 \omega _0)+\omega _0 (a_3 \cos (\kappa \tau _0 \omega _0)+a_2 \bar{G})). \end{aligned}$$

Hence, using these coefficients and (52), (53), one obtains equations of the form (54), (55).